浙江省台州市三区三校（椒江五中）2021届九年级上学期数学期...

更新时间：2024-07-31 浏览次数：262 类型：期中考试

一、选择题（每题4分，共40分）

1. (2020九上·台州期中) 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（）

A . 赵爽弦图 B . 笛卡尔心型曲线 C . 科克曲线 D . 波那契螺旋线

答案解析收藏纠错 + 选题
2. (2020九上·台州期中) 一元二次方程x²-5x+6=0的解为（）

A . X1=2，x2= -3 B . x1= -2, x2=-3 C . x1=-2,x2=-3 D . x1=2,x2=3

答案解析收藏纠错 + 选题
3. (2022·罗山模拟) 二次函数 $\text{[math]}$ 的图象经过点（0，2），则a+b的值是（）

A . -3 B . -1 C . 2 D . 3

答案解析收藏纠错 + 选题
4. (2020九上·台州期中) 如图，已知△ABC内接于⊙O，∠C=45∘，AB=4，则⊙O的半径为（）

A . $\text{[math]}$ B . 4 C . $\text{[math]}$ D . 5

答案解析收藏纠错 + 选题
5. (2020九上·台州期中) 如图，△ABC和△A₁B₁C₁关于点E成中心对称，则点E坐标是（）

A . (−3，−1) B . (−3，−3) C . (−3，0) D . (−4，−1)

答案解析收藏纠错 + 选题

6. (2020九上·台州期中) 已知一次函数y1=kx+m(k≠0)和二次函数y2=ax²+bx+c(a≠0)部分自变量和对应的函数值如表：

x	…	−1	0	2	4	5	…
y1	…	0	1	3	5	6	…
y2	…	0	−1	0	5	9	…

当y2>y1时，自变量x的取值范围是（）

A . -1＜x＜2 B . 4＜x＜5 C . x＜-1或x＞5 D . x＜-1或x＞4

答案解析收藏纠错 + 选题

7. (2020九上·台州期中) 如图，PA，PB分别切⊙O与点A，B，MN切⊙O于点C，分别交PA，PB于点M，N，若PA=7.5cm，则△PMN的周长是（）

A . 7.5cm B . 10cm C . 12.5cm D . 15cm

答案解析收藏纠错 + 选题
8. (2020九上·台州期中) 如图，Rt△ABC中，∠BAC=90°，AB=AC，将△ABC绕点C顺时针旋转40°得到△A＇B＇C，CB＇与AB相交于点D，连接AA＇，则∠B＇A＇A的度数为（）

A . 10° B . 15° C . 20° D . 30°

答案解析收藏纠错 + 选题
9. (2020九上·惠来期末) 如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E.F分别在BC和CD上，下列结论：
①CE=CF；②∠AEB=75°；③BE+DF=EF；④正方形对角线AC=1+ $\text{[math]}$ ，其中正确的序号是( ）

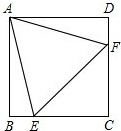
A . ①②④ B . ①② C . ②③④ D . ①③④

答案解析收藏纠错 + 选题
10. (2020九上·台州期中) 已知二次函数y=x²−bx+1(−1⩽b⩽1)，当b从−1逐渐变化到1的过程中，它所对应的抛物线位置也随之变动。下列关于抛物线的移动方向的描述中，正确的是（）

A . 先往左上方移动，再往左下方移动； B . 先往左下方移动，再往左上方移动； C . 先往右上方移动，再往右下方移动； D . 先往右下方移动，再往右上方移动。

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题5分，共30分）

11. (2020九上·台州期中) 若关于x的方程x²+ax-2=0有一个根是1，则a=

答案解析收藏纠错 + 选题
12. (2023九上·黄岩期中) 将抛物线y＝x²＋1向下平移3个单位长度得到的抛物线的解析式为.

答案解析收藏纠错 + 选题
13. (2023九上·黄岩期中) 由于受“一带一路”国家战略策略的影响，某种商品的进口关税连续两次下调，由4000美元下调至2560美元，则平均每次下调的百分率为.

答案解析收藏纠错 + 选题
14. (2020九上·台州期中) 如图，直线AB，CD相交于点O，∠AOC=30°，半径为1cm的的圆心P在射线OA上，且与点O的距离为6cm，⊙P以1cm/s的速度沿由A向B的方向移动，那么⊙P与直线CD相切时，圆心P的运动时间为.

答案解析收藏纠错 + 选题
15. (2020九上·台州期中) 如图，在△ABC中，AB=10，AC=8，BC=6，经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q，则线段PQ长度的最小值是

答案解析收藏纠错 + 选题
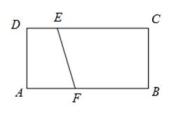
16. (2023九下·杭州月考) 如图，在矩形ABCD中，AB=4，AD=2，点E在CD上，DE=1，点F是边AB上一动点，以EF为斜边作Rt△EFP．若点P在矩形ABCD的边上，且这样的直角三角形恰好有两个，则AF的值是。

答案解析收藏纠错 + 选题

三、解答题（共80分，第17-19题各8分，第20,21题各9分，第22,23题各12分，第24题14分）

17. (2020九上·台州期中) 解下列方程
1. （1） x²-4x-5=0
2. （2） 2（x-3）²=3（x-3）
答案解析收藏纠错 + 选题
18. (2020九上·台州期中) 图①，图②，图③均为4×4的正方形网格，每个小正方形的顶点称为格点，小正方形的边长都为1.线段AB的端点均在格点上.按要求在图①，图②，图③中画图.
1. （1）在图①中，以线段AB为斜边画一个等腰直角三角形，且直角的顶点为格点；
2. （2）在图②中，以线段AB为斜边画一个直角三角形，使其面积为2，且直角的顶点为格点；
3. （3）在图③中，画一个四边形，使所画四边形是中心对称图形，不是轴对称图形，且其余两个顶点均为格点.
答案解析收藏纠错 + 选题
19. (2020九上·台州期中) 为响应区“美丽台州，美化环境”的号召，某校开展“美丽台州清洁校园”的活动，该校经过精心设计，计算出需要绿化的面积为498m² ，绿化150m²后，为了更快的完成该项绿化工作，将每天的工作量提高为原来的1.2倍．结果一共用20天完成了该项绿化工作．
1. （1）该项绿化工作原计划每天完成多少m²？
2. （2）在绿化工作中有一块面积为170m²的矩形场地，矩形的长比宽的2倍少3m，请问这块矩形场地的长和宽各是多少米？
答案解析收藏纠错 + 选题
20. (2020九上·台州期中) 如图，已知AB是⊙O中一条固定的弦，点C是优弧AB上一个动点(点C不与A，B重合).
1. （1）设∠ACB的角平分线与劣弧AB交于点P，试猜想点P在AB⌢上的位置是否会随点C的运动而发生变化?请说明理由；
2. （2）如图②，设A′B′=8，⊙O的半径为5，在(1)的条件下，四边形ACBP的面积是否为定值?若是定值，请求出这个定值；若不是定值，试确定四边形A′C′B′P′的面积的取值范围.
答案解析收藏纠错 + 选题
21. (2020九上·台州期中) 一座拱桥的轮廓是抛物线型(如图1所示)，拱高6m，跨度20m，相邻两支柱间的距离均为5m.
1. （1）将抛物线放在所给的直角坐标系中(如图2所示)，其表达式是 $\text{[math]}$ 的形式。请根据所给的数据求出a，c的值。
2. （2）求支柱MN的长度。
3. （3）拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带)，其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由。
答案解析收藏纠错 + 选题
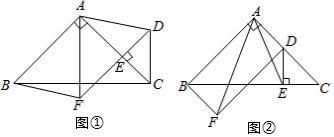
22. (2020九上·台州期中) 如图①，在△ABC中，∠BAC=90∘，AB=AC，点E在AC上(且不与点A，C重合)，在△ABC的外部作△CED，使∠CED=90∘，DE=CE，连接AD，分别以AB，AD为邻边作平行四边形ABFD，连接AF.
1. （1）请直接写出线段AF，AE的数量关系；
2. （2）将△CED绕点C逆时针旋转，当点E在线段BC上时，如图②，连接AE，请判断线段AF，AE的数量关系，并证明你的结论。
答案解析收藏纠错 + 选题
23. (2020九上·台州期中) 如图，已知AB是⊙O的直径，C是圆周上的动点，P是优弧ABC的中点.
1. （1）如图①，求证：OP∥BC；
2. （2）如图②，PC交AB于点D，当△ODC是等腰三角形时，求∠PAO的度数.
答案解析收藏纠错 + 选题
24. (2020九上·台州期中) 定义：对于给定的两个函数，任取自变量x的一个值，当 $\text{[math]}$ 时，它们对应的函数值互为相反数；当 $\text{[math]}$ 时，它们对应的函数值相等，我们称这样的两个函数互为相关函数。例如：一次函数 $\text{[math]}$ ，它们的相关函数为 $\text{[math]}$ 。
1. （1）已知点 $\text{[math]}$ 在一次函数 $\text{[math]}$ 的相关函数的图象上，求a的值。
2. （2）已知二次函数 $\text{[math]}$ 。
  ①当点 $\text{[math]}$ 在这个函数的相关函数的图象上时，求m的值；
  
  ②当 $\text{[math]}$ 时，求函数 $\text{[math]}$ 的相关函数的最大值和最小值。
3. （3）在平面直角坐标系中，点M，N的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ，连结MN。直接写出线段MN与二次函数 $\text{[math]}$ 的相关函数的图象有两个公共点时n的取值范围。
答案解析收藏纠错 + 选题