![]()
![]()
![]()
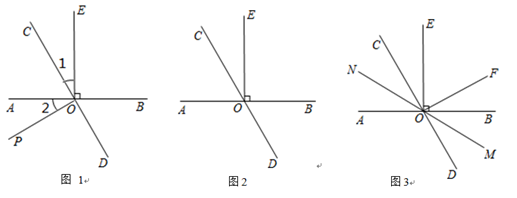
①当 时,求t的值;
②当 时,请直接写出t的值.
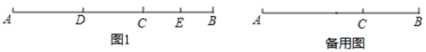
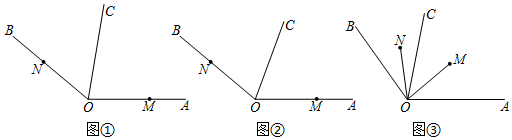
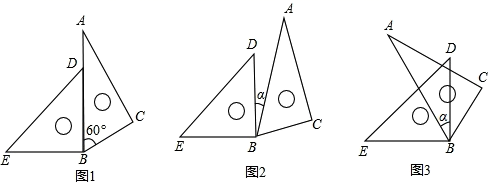
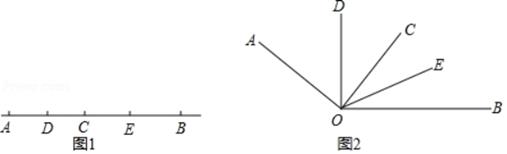
①如图1,当E为BC中点时,求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,求AD的长;
![]()
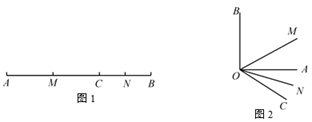
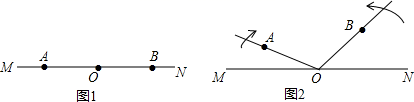
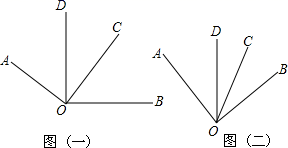
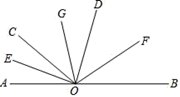
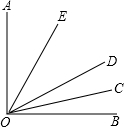
①直接写出图中两个相等的锐角:=;
②如果∠COD=40°,则∠AOB=,若∠AOB=150°,则∠COD=;
③猜想∠AOB+∠DOC=°,请说明理由.

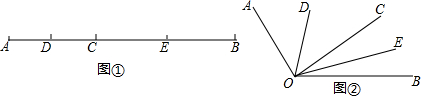
D、OE分别平分∠AOC和∠BOC,试说明∠DOE的度数与射线OC的位置无关.