2016年浙江省金华市中考数学试卷

更新时间：2024-07-12 浏览次数：1363 类型：中考真卷

一、选择题

1. (2016·金华) 实数﹣ $\text{[math]}$ 的绝对值是（）

A . 2 B . $\text{[math]}$ C . ﹣ $\text{[math]}$ D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2016·金华)
若实数a，b在数轴上的位置如图所示，则下列判断错误的是（）

A . a＜0 B . ab＜0 C . a＜b D . a，b互为倒数

答案解析收藏纠错 + 选题
3. (2021七上·上思期中)
如图是加工零件的尺寸要求，现有下列直径尺寸的产品（单位：mm），其中不合格的是（）

A . Φ45.02 B . Φ44.9 C . Φ44.98 D . Φ45.01

答案解析收藏纠错 + 选题
4. (2020九下·吉林月考)
从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体，得到的几何体如图所示，则该几何体的左视图正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024八下·越城期末) 一元二次方程x²﹣3x﹣2=0的两根为x₁ ， x₂ ，则下列结论正确的是（）

A . x₁=﹣1，x₂=2 B . x₁=1，x₂=﹣2 C . x₁+x₂=3 D . x₁x₂=2

答案解析收藏纠错 + 选题
6. (2023八上·平潭月考)
如图，已知∠ABC=∠BAD，添加下列条件还不能判定△ABC≌△BAD的是（）

A . AC=BD B . ∠CAB=∠DBA C . ∠C=∠D D . BC=AD

答案解析收藏纠错 + 选题
7. (2016·金华) 小明和小华参加社会实践活动，随机选择“打扫社区卫生”和“参加社会调查”其中一项，那么两人同时选择“参加社会调查”的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2016·金华)
一座楼梯的示意图如图所示，BC是铅垂线，CA是水平线，BA与CA的夹角为θ．现要在楼梯上铺一条地毯，已知CA=4米，楼梯宽度1米，则地毯的面积至少需要（）

A . $\text{[math]}$ 米² B . $\text{[math]}$ 米² C . （4+ $\text{[math]}$ ）米² D . （4+4tanθ）米²

答案解析收藏纠错 + 选题
9. (2021九上·金华月考)
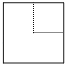
足球射门，不考虑其他因素，仅考虑射点到球门AB的张角大小时，张角越大，射门越好．如图的正方形网格中，点A，B，C，D，E均在格点上，球员带球沿CD方向进攻，最好的射点在（）

A . 点C B . 点D或点E C . 线段DE（异于端点）上一点 D . 线段CD（异于端点）上一点

答案解析收藏纠错 + 选题
10. (2016·金华)
在四边形ABCD中，∠B=90°，AC=4，AB∥CD，DH垂直平分AC，点H为垂足．设AB=x，AD=y，则y关于x的函数关系用图象大致可以表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

11. (2016·金华) 不等式3x+1＜﹣2的解集是．

答案解析收藏纠错 + 选题
12. 能够说明“ $\text{[math]}$ =x不成立”的x的值是（写出一个即可）．

答案解析收藏纠错 + 选题
13. (2022八下·南开期末)
为监测某河道水质，进行了6次水质检测，绘制了如图的氨氮含量的折线统计图．若这6次水质检测氨氮含量平均数为1.5mg/L，则第3次检测得到的氨氮含量是mg/L．

答案解析收藏纠错 + 选题
14. (2016·金华)
如图，已知AB∥CD，BC∥DE．若∠A=20°，∠C=120°，则∠AED的度数是．

答案解析收藏纠错 + 选题
15. (2023九下·西湖月考)
如图，Rt△ABC纸片中，∠C=90°，AC=6，BC=8，点D在边BC 上，以AD为折痕△ABD折叠得到△AB′D，AB′与边BC交于点E．若△DEB′为直角三角形，则BD的长是．

答案解析收藏纠错 + 选题
16. (2016·金华)
由6根钢管首尾顺次铰接而成六边形钢架ABCDEF，相邻两钢管可以转动．已知各钢管的长度为AB=DE=1米，BC=CD=EF=FA=2米．（铰接点长度忽略不计）
1. （1）转动钢管得到三角形钢架，如图1，则点A，E之间的距离是米．
2. （2）转动钢管得到如图2所示的六边形钢架，有∠A=∠B=∠C=∠D=120°，现用三根钢条连接顶点使该钢架不能活动，则所用三根钢条总长度的最小值是米．
答案解析收藏纠错 + 选题

三、解答题

17. (2016·金华) 计算： $\text{[math]}$ ﹣（﹣1）²⁰¹⁶﹣3tan60°+（﹣2016）⁰ ．

答案解析收藏纠错 + 选题
18. (2016·金华) 解方程组 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2022·衢州模拟)
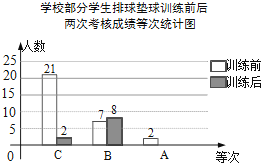
某校组织学生排球垫球训练，训练前后，对每个学生进行考核．现随机抽取部分学生，统计了训练前后两次考核成绩，并按“A，B，C”三个等次绘制了如图不完整的统计图．试根据统计图信息，解答下列问题：
1. （1）抽取的学生中，训练后“A”等次的人数是多少？并补全统计图．
2. （2）若学校有600名学生，请估计该校训练后成绩为“A”等次的人数．
答案解析收藏纠错 + 选题
20. (2016·金华)
如图1表示同一时刻的韩国首尔时间和北京时间，两地时差为整数．
1. （1）设北京时间为x（时），首尔时间为y（时），就0≤x≤12，求y关于x的函数表达式，并填写下表（同一时刻的两地时间）．
  北京时间
  7：30
  11：15
  2：50
  首尔时间
  8：30
  12：15
  3：50
2. （2）如图2表示同一时刻的英国伦敦时间（夏时制）和北京时间，两地时差为整数．如果现在伦敦（夏时制）时间为7：30，那么此时韩国首尔时间是多少？
答案解析收藏纠错 + 选题
21. (2016·金华)
如图，直线y= $\text{[math]}$ x﹣ $\text{[math]}$ 与x，y轴分别交于点A，B，与反比例函数y= $\text{[math]}$ （k＞0）图象交于点C，D，过点A作x轴的垂线交该反比例函数图象于点E．
1. （1）求点A的坐标．
2. （2）若AE=AC．
  ①求k的值．
  ②试判断点E与点D是否关于原点O成中心对称？并说明理由．
答案解析收藏纠错 + 选题
22. (2016·金华)
四边形ABCD的对角线交于点E，有AE=EC，BE=ED，以AB为直径的半圆过点E，圆心为O．
1. （1）利用图1，求证：四边形ABCD是菱形．
2. （2）如图2，若CD的延长线与半圆相切于点F，已知直径AB=8．
  ①连结OE，求△OBE的面积．
  ②求弧AE的长．
答案解析收藏纠错 + 选题
23. (2016·金华)
在平面直角坐标系中，点O为原点，平行于x轴的直线与抛物线L：y=ax²相交于A，B两点（点B在第一象限），点D在AB的延长线上．
1. （1）已知a=1，点B的纵坐标为2．
  ①如图1，向右平移抛物线L使该抛物线过点B，与AB的延长线交于点C，求AC的长．
  ②如图2，若BD= $\text{[math]}$ AB，过点B，D的抛物线L₂ ，其顶点M在x轴上，求该抛物线的函数表达式．
2. （2）如图3，若BD=AB，过O，B，D三点的抛物线L₃ ，顶点为P，对应函数的二次项系数为a₃ ，过点P作PE∥x轴，交抛物线L于E，F两点，求 $\text{[math]}$ 的值，并直接写出 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
24. (2016·金华)
在平面直角坐标系中，点O为原点，点A的坐标为（﹣6，0）．如图1，正方形OBCD的顶点B在x轴的负半轴上，点C在第二象限．现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG．
1. （1）如图2，若α=60°，OE=OA，求直线EF的函数表达式．
2. （2）若α为锐角，tanα= $\text{[math]}$ ，当AE取得最小值时，求正方形OEFG的面积．
3. （3）当正方形OEFG的顶点F落在y轴上时，直线AE与直线FG相交于点P，△OEP的其中两边之比能否为 $\text{[math]}$ ：1？若能，求点P的坐标；若不能，试说明理由
答案解析收藏纠错 + 选题