| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 4 | 1 | 0 | 1 | 4 | … |
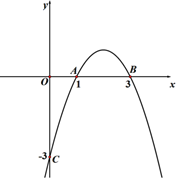
点 、
在函数的图象上,则当1<x1<2,3<x2<4时,
与
的大小关系正确的是( )
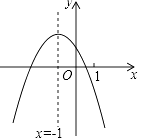
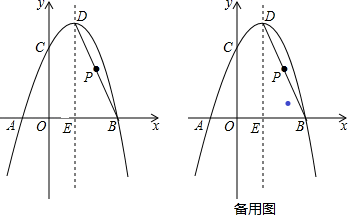
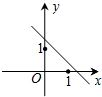
已知函数y=(x﹣a)(x﹣b)(其中a>b)的图象如下面右图所示,则函数y=ax+b的图象可能正确的是( )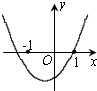
 B .
B . 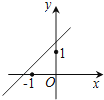 C .
C . 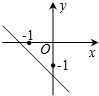 D .
D . 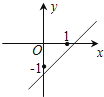

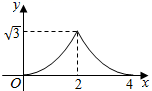 B .
B . 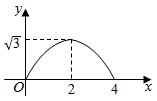 C .
C . 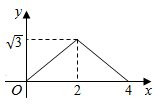 D .
D . 
|
温度t/℃ |
-4 |
-2 |
0 |
1 |
4 |
|
植物高度增长量l/mm |
41 |
49 |
49 |
46 |
25 |
科学家经过猜想、推测出l与t之间是二次函数关系.由此可以推测最适合这种植物生长的温度为℃.