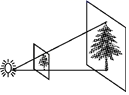






( 1 )画出△ABC向下平移4个单位长度得到的△A1B1C1;
( 2 )以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ▲ ;
( 3 )△A2B2C2的面积是 ▲ 平方单位.



|
普通口罩 |
N95口罩 |
|
|
进价(元/包) |
8 |
20 |


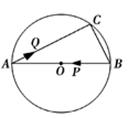
①点M( ,0) ▲ ⊙O的“完美点”,点(﹣
,﹣
) ▲ ⊙O的“完美点”;(填“是”或者“不是”)
②若⊙O的“完美点”P在直线y= x上,求PO的长及点P的坐标;