浙江省台州市椒江区第二中学2020-2021学年八年级上学期...

更新时间：2020-12-25 浏览次数：185 类型：期中考试

一、单选题

1. (2019·北京) 下列倡导节约的图案中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. 现要用三根木棒搭一个三角形，已知其中两根木棒的长分别是3cm和5cm，那么第三根的长可以是（）

A . 7cm B . 8cm C . 9cm D . 10cm

答案解析收藏纠错 + 选题
3. (2016九上·海南期中) 已知图中的两个三角形全等，则∠α的度数是（）

A . 72° B . 60° C . 58° D . 50°

答案解析收藏纠错 + 选题
4. 正十二边形的外角和的度数为（）

A . 1800° B . 720° C . 360° D . 180°

答案解析收藏纠错 + 选题
5. (2020七下·南岸期末) 为了测量池塘两侧A，B两点间的距离，在地面上找一点C，连接AC，BC，使∠ACB=90°，然后在BC的延长线上确定点D，使CD=BC，得到△ABC≌△ADC，通过测量AD的长，得AB的长.那么△ABC≌△ADC的理由是（）

A . SAS B . AAS C . ASA D . SSS

答案解析收藏纠错 + 选题
6. (2020八下·邵阳期末) 如图，OD平分∠AOB，DE⊥AO于点E，DE=4，点F是射线OB上的任意一点，则DF的长度不可能是（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
7. 如图，已知AD是△ABC的边BC上的中线，CE是△ADC的边AD上的中线，若△ABD的面积为16cm² ，则△CDE的面积为（）

A . 32 cm² B . 16cm² C . 8cm² D . 4cm²

答案解析收藏纠错 + 选题
8. 如图等边△ABC边长为1cm，D、E分别是AB、AC上两点，将△ADE沿直线DE折叠，点A落在 $\text{[math]}$ 处，A在△ABC外，则阴影部分图形周长为（）

A . 1cm B . 1.5cm C . 2cm D . 3cm

答案解析收藏纠错 + 选题
9. (2020八上·惠州月考) 在如图所示的 6×6 网格中，△ABC是格点三角形（即顶点恰好是网格线的交点），则与△ABC有一条公共边且全等（不含△ABC）的所有格点三角形的个数（）

A . 3 个 B . 4 个 C . 6 个 D . 7 个

答案解析收藏纠错 + 选题
10. 如图，已知等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，下面的结论：①∠APO+∠DCO=30°；②△OPC是等边三角形；③AC=AO+AP；④S_△_ABC=S四边形AOCP，其中正确的个数是（）

A . ①②③ B . ①③④ C . ②③④ D . ①②③④

答案解析收藏纠错 + 选题

二、填空题

11. (2019八上·天台月考) 人字梯中间一般会设计一”拉杆”，这样做的数学道理是．

答案解析收藏纠错 + 选题
12. 已知点A（a，5）与点B（2，5）关于y轴对称，则a=.

答案解析收藏纠错 + 选题
13. 已知：如图，△ABC和△BAD中，∠C=∠D=90°，再添加一个条件就可以判断△ABC≌△BAD.

答案解析收藏纠错 + 选题
14. 如图，将长方形纸片ABCD折叠，使顶点A，C重合，折痕为EF.若AE=4，则AF=.

答案解析收藏纠错 + 选题
15. (2020·铁岭) 如图，以 $\text{[math]}$ 为边，在 $\text{[math]}$ 的同侧分别作正五边形 $\text{[math]}$ 和等边 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是.

答案解析收藏纠错 + 选题
16. 如图，在△ABC中，AD⊥BC于D，BD=AC+CD，设∠CAD=α，则∠B=.（用含α的式子表示）

答案解析收藏纠错 + 选题

三、解答题

17. 已知，在10×10网格中建立如图所示的平面直角坐标系，△ABC是格点三角形（三角形的顶点是网格线的交点）.

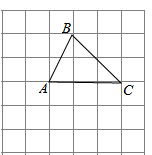
（ 1 ）画出△ABC关于y轴对称的△A₁B₁C₁ ，并写出A₁ ， B₁ ， C₁的坐标；

（ 2 ）求△ABC的面积.

答案解析收藏纠错 + 选题
18. 如图，在△ABC中，AB=AC，DE是边AB的垂直平分线，交AB于E，交CA的延长线于D，交BC于F点，连接BD.
1. （1）求证：△ABD为等腰三角形；
2. （2）连接AF，若∠BAC=140°，求证：∠AFC=∠DBA.
答案解析收藏纠错 + 选题
19. 如图，在△ABC和△DEF中，BM，EN分别是AC，DF边上的中线.
1. （1）若△ABC≌△DEF，求证：BM=EN；
2. （2）若AB=8，BC=6，求BM的取值范围.
答案解析收藏纠错 + 选题
20. (2018八上·句容月考) 如图是小朋友荡秋千的侧面示意图，静止时秋千位于铅垂线BD上，转轴B到地面的距离BD=3m．小亮在荡秋千过程中，当秋千摆动到最高点A时，测得点A到BD的距离AC=2m，点A到地面的距离AE=1.8m；当他从A处摆动到A′处时，有A'B⊥AB．
1. （1）求A′到BD的距离；
2. （2）求A′到地面的距离．
答案解析收藏纠错 + 选题
21. 定义：到三角形的两个顶点距离相等的点，叫做三角形的“中垂心”.如图1，在△ABC中，PA=PB，则点P叫做△ABC的“中垂心”.
1. （1）根据定义，中垂心可能在三角形顶点处的三角形有（举一个例子即可）；
2. （2）应用：如图2；在△ABC中，请画出“中垂心”P，使PA=PB=PC.（保留作图痕迹，不写画法）
3. （3）探究：①如图3，已知△ABC为直角三角形，∠C=90°，∠ABC=60°，AC= $\text{[math]}$ ，“中垂心”P在AC边上，求PA的长.
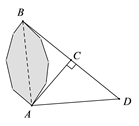
  ②如图4，若PA=PB且“中垂心”P在△ABC内部，总有AC+BC $\text{[math]}$ 2AP，请说明理由.
答案解析收藏纠错 + 选题
22. 如图
1. （1）性质：角平分线上的点到角两边的距离相等，如图1：OP平分∠MON，PC⊥OM于C，PB⊥ON于B，则PBPC（填“ $\text{[math]}$ ”“ $\text{[math]}$ ”或“=”）；
2. （2）探索：如图2，小明发现，在△ABC中，AD是∠BAC的平分线，则 $\text{[math]}$ ，请帮小明说明原因.
3. （3）应用：如图3，在小区三条交叉的道路AB，BC，CA上各建一个菜鸟驿站D，P，E，工作人员每天来回的路径为P→D→E→P，
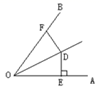
  ①问点P应选在BC的何处时，才能使PD+DE+PE最小？
  
  ②若∠BAC=30°，S△ABC=10，BC=5，则PD+DE+PE的最小值是多少？
答案解析收藏纠错 + 选题