25.
(2022八下·五华期末)
定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.如图1,∠
ABC=∠
ADC=90°,四边形
ABCD是损矩形,则该损矩形的直径是线段
AC . 同时我们还发现损矩形中有公共边的两个三角形角的特点:在公共边的同侧的两个角是相等的.如图1中:△
ABC和△
ABD有公共边
AB , 在
AB同侧有∠
ADB和∠
ACB , 此时∠
ADB=∠
ACB;再比如△
ABC和△
BCD有公共边
BC , 在
CB同侧有∠
BAC和∠
BDC , 此时∠
BAC=∠
BDC .
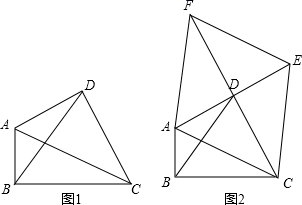


;⑤当BP=9时,BE•EF=108.