江西省赣州市2020-2021学年九年级上学期数学第二次月考...

更新时间：2024-07-13 浏览次数：227 类型：月考试卷

一、单选题

1. (2020九上·赣州月考) 下列事件中，是随机事件的是（）

A . 明天太阳从西边出来 B . 打开电视，正在播放《江西新闻》 C . 南昌是江西的省会 D . 小明跑完1000米所用的时间恰好为1分钟

答案解析收藏纠错 + 选题
2. (2020·中模拟) 江西景德镇的青花瓷是中华陶瓷工艺的珍品，下列青花瓷上的青花图案既是轴对称图形又是中心对称图形的是(　　)

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2020九上·赣州月考) 已知半径为10的⊙O和直线l上一点A，且 $\text{[math]}$ ，则直线l与⊙O的位置关系是（）

A . 相切 B . 相交 C . 相交或相离 D . 相切或相交

答案解析收藏纠错 + 选题
4. (2020九上·赣州月考) 如图，AB是⊙O的直径，C、D为⊙O上的点，弧AD＝弧CD ，若∠CAB＝40°，则∠CAD＝（）

A . 30° B . 40° C . 50° D . 25°

答案解析收藏纠错 + 选题
5. (2024九上·钦州月考) 当 $\text{[math]}$ 时，关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的根的情况为（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 没有实数根 D . 无法确定

答案解析收藏纠错 + 选题
6. (2024九下·上高模拟) 对于抛物线y＝ax²+4ax﹣m（a≠0）与x轴的交点为A(﹣1，0)，B(x₂ ， 0)，则下列说法：
①一元二次方程ax²+4ax﹣m＝0的两根为x₁＝﹣1，x₂＝﹣3；

②原抛物线与y轴交于点C ， CD∥x轴交抛物线于D点，则CD＝4；

③点E(1，y₁)、点F(﹣4，y₂)在原抛物线上，则y₁＞y₂；

④抛物线y＝﹣ax²﹣4ax+m与原抛物线关于x轴对称．其中正确的有（　　）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题

二、填空题

7. (2020九上·赣州月考) 把抛物线 $\text{[math]}$ 向上平移2个单位，所得抛物线是．

答案解析收藏纠错 + 选题
8. (2020九上·赣州月考) 已知a、b是一元二次方程x²－2x－2020=0的两个根，则2a+2b－ab的值为．

答案解析收藏纠错 + 选题
9. (2020九上·赣州月考) 《九章算术》是我国古代内容极为丰富的数学名著．书中有下面问题“今有勾八步，股十五步，问勾中容圆径几何．”其意思是：“今有直角三角形，勾（短直角边）长为8步，股（长直角边）长为15步，问该直角三角形能容纳的圆形（内切圆）直径是多少？”．请你计算其结果为步．

答案解析收藏纠错 + 选题
10. (2022·淄博模拟) 如图，在正六边形ABCDEF中，分别以C ， F为圆心，以边长为半径作弧，图中阴影部分的面积为24π，则正六边形的边长为．

答案解析收藏纠错 + 选题
11. (2024九上·云梦月考) 加工爆米花时，爆开且不糊的颗粒的百分比称为“可食用率”.在特定条件下，可食用率 $\text{[math]}$ 与加工时间 $\text{[math]}$ （单位： $\text{[math]}$ ）满足函数表达式 $\text{[math]}$ ，则最佳加工时间为 $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2020九上·赣州月考) $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点O是AB的中点，将OB绕点O向三角形外部旋转 $\text{[math]}$ 角时（ $\text{[math]}$ ），得到OP ，当 $\text{[math]}$ 恰为等腰三角形时， $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

三、解答题

13. (2020九上·赣州月考)
1. （1）解方程： $\text{[math]}$ ；
2. （2）如图所示，在 $\text{[math]}$ 纸片中， $\text{[math]}$ ，将 $\text{[math]}$ 纸片绕点A按逆时针方向旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，此时AD边经过点C ，连接BD ，若 $\text{[math]}$ 的度数为 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
14. (2020九上·赣州月考) 已知关于x的二次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求b、c的值；
2. （2）求出此二次函数的图象的顶点坐标及其与y轴的交点坐标．
答案解析收藏纠错 + 选题
15. (2020九上·赣州月考) 如图，△ABC是⊙O的内接三角形，∠ABC＝45°，请用无刻度的直尺按要求作图.

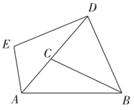
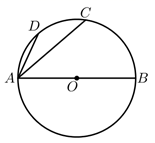
⑴如图1，请在图1中画出弦CD，使得CD＝AC．

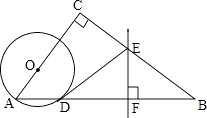
⑵如图2，AB是⊙O的直径，AN是⊙O的切线，点B，C，N在同一条直线上请在图中画出△ABN的边AN上的中线BD．

答案解析收藏纠错 + 选题
16. (2021九上·西湖期中) 随着信息技术的迅猛发展，移动支付如今已成为一种世界性的时代趋势．在一次购物中，刘老师和王老师都想从“微信”“支付宝”“银行卡”三种支付方式中选一种方式进行支付．
1. （1）王老师选择“微信”支付的概率是；
2. （2）请用列表法或画树状图法，求两位老师恰好一人选择“微信”支付，一人选择“银行卡”支付的概率．
答案解析收藏纠错 + 选题
17. (2020九上·赣州月考)
如图，∠C=90°，以AC为半径的圆C与AB相交于点D．若AC=3，CB=4，求BD长．

答案解析收藏纠错 + 选题
18. (2020九上·赣州月考) 如图所示的正方形网格中（每个小正方形的边长是1，小正方形的顶点叫作格点），△ABC的顶点均在格点上，请在所给平面直角坐标系中按要求画图和解答下列问题：
1. （1） ①以点C为旋转中心，将△ABC绕点C顺时针旋转90°得△CA₁B₁ ，画出△CA₁B₁；
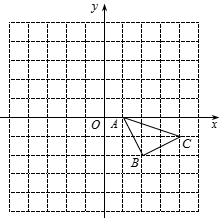
  ②作出△ABC关于点A成中心对称的△AB₂C₂；
2. （2）设AC₂与y轴交于点D ，则△B₁DC的面积为．
答案解析收藏纠错 + 选题
19. (2021九上·四会月考) 关于x的一元二次方程 $\text{[math]}$ 有两个实数根 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求k的取值范围；
2. （2）是否存在实数k ，使得 $\text{[math]}$ 和 $\text{[math]}$ 互为相反数？若存在，请求出k的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题
20. (2020九上·赣州月考) 某地摊上的一种玩具，已知其进价为50元个，试销阶段发现将售价定为80元/个时，每天可销售20个，后来为了扩大销售量，适当降低了售价，销售量y(个)与降价x(元)的关系如图所示．
1. （1）
  求销量y与降价x之间的关系式；
2. （2）该玩具每个降价多少元，可以恰好获得750元的利润？
3. （3）若要使得平均每天销售这种玩具的利润W最大，则每个玩具应该降价多少元？最大的利润W为多少元？
答案解析收藏纠错 + 选题
21. (2022九上·自贡期末) 如图，在△ABC中，∠C=90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD的垂直平分线交BC于点E，交BD于点F，连接DE．
1. （1）判断直线DE与⊙O的位置关系，并说明理由；
2. （2）若AC=6，BC=8，OA=2，求线段DE的长．
答案解析收藏纠错 + 选题
22. (2020九上·赣州月考) 已知抛物线 $\text{[math]}$ 中（a ， b是常数）与y轴的交点为A ，点A与点B关于抛物线的对称轴对称，二次函数 $\text{[math]}$ 中（b ， c是常数）的自变量x与函数值y的部分对应值如下表：，

$\text{[math]}$

…

$\text{[math]}$

0

1

3

4

…

$\text{[math]}$

…

8

0

0

…
1. （1）下列结论正确的是
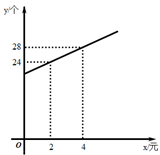
  A ．抛物线的对称轴是 $\text{[math]}$
  
  B ．当 $\text{[math]}$ 时，y有最大值 $\text{[math]}$
  
  C ．当 $\text{[math]}$ 时，随x的增大而增大
  
  D ．点A的坐标是 $\text{[math]}$ ，点B的坐标是 $\text{[math]}$
2. （2）求二次函数 $\text{[math]}$ 的解析式
3. （3）已知点 $\text{[math]}$ 在抛物线 $\text{[math]}$ 上，设 $\text{[math]}$ 的面积为S ，求S与m的函数关系式画出函数图象．并利用函数图象说明S是否存在最大值，为什么？
答案解析收藏纠错 + 选题
23. (2020九上·赣州月考) 问题背景：如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，四边形 $\text{[math]}$ 是正方形，求图中阴影部分的面积.
1. （1）发现：如图2，小芳发现，只要将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转一定的角度到达 $\text{[math]}$ ，就能将阴影部分转化到一个三角形里，从而轻松解答.根据小芳的发现，可求出图1中阴影部分的面积为；（直接写出答案）
2. （2）应用：如图3，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ，若四边形 $\text{[math]}$ 的面积为16，试求出 $\text{[math]}$ 的长；
3. （3）拓展：如图4，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，以 $\text{[math]}$ 为顶点作 $\text{[math]}$ 为 $\text{[math]}$ 角，角的两边分别交 $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 两点，连接 $\text{[math]}$ ，请直接写出线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系.
答案解析收藏纠错 + 选题