广西壮族自治区南宁市第四十七中学2020-2021学年八年级...

更新时间：2021-03-10 浏览次数：166 类型：月考试卷

一、单选题

1. 2020的相反数是（）

A . 2020 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 下列汽车标志中，既是中心对称图形又是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. 氢原子的半径大约是 $\text{[math]}$ ，将数据0.0000077用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. 下列调查中，最适宜采用全面调查方式的是（）

A . 调查某市成年人的学历水平 B . 调查某批次日光灯的使用寿命 C . 调查市场上矿泉水的质量情况 D . 了解某个班级学生的视力情况

答案解析收藏纠错 + 选题
5. (2019·沈阳) 已知一次函数y＝（k+1）x+b的图象如图所示，则k的取值范围是（）

A . k＜0 B . k＜﹣1 C . k＜1 D . k＞﹣1

答案解析收藏纠错 + 选题
6. 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. 二次函数 $\text{[math]}$ 有（）

A . 最大值 $\text{[math]}$ B . 最小值 $\text{[math]}$ C . 最大值 $\text{[math]}$ D . 最小值 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020·萧山模拟) 如图，⊙O的半径为2，点A为⊙O上一点，OD⊥弦BC于D，如果∠BAC＝60°，那么OD的长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . 2

答案解析收藏纠错 + 选题
9. (2018·阿城模拟) 如图，点F是▱ABCD的边CD上一点，直线BF交AD的延长线于点E，则下列结论错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

10. (2019·台州) 一道来自课本的习题：

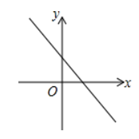
从甲地到乙地有一段上坡与一段平路，如果保持上坡每小时走3km，平路每小时走4km，下坡每小时走5km，那么从甲地到乙地需54min，从乙地到甲地需42min，甲地到乙地全程是多少？

小红将这个实际问题转化为二元一次方程组问题，设未知数x，y，已经列出一个方程 $\text{[math]}$ ，则另一个方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

11. (2020九上·南宁期末) 如图，正方形 $\text{[math]}$ 的边长为 $\text{[math]}$ ，对角线 $\text{[math]}$ 相交于点 $\text{[math]}$ ，将直角三角板的直角顶点放在点 $\text{[math]}$ 处，两直角边分别与 $\text{[math]}$ 重叠，当三角板绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 角 $\text{[math]}$ 时，两直角边与正方形的边 $\text{[math]}$ 交于 $\text{[math]}$ 两点，则四边形 $\text{[math]}$ 的周长（）

A . 先变小再变大 B . 先变大再变小 C . 始终不变 D . 无法确定

答案解析收藏纠错 + 选题
12. (2017·葫芦岛) 如图，菱形ABCD的边长为2，∠A=60°，点P和点Q分别从点B和点C出发，沿射线BC向右运动，且速度相同，过点Q作QH⊥BD，垂足为H，连接PH，设点P运动的距离为x（0＜x≤2），△BPH的面积为S，则能反映S与x之间的函数关系的图象大致为（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

13. 不等式 $\text{[math]}$ 的解集是.

答案解析收藏纠错 + 选题
14. 若分式 $\text{[math]}$ 的值为0，则x的值为.

答案解析收藏纠错 + 选题
15. 如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径 $\text{[math]}$ ，扇形的圆心角 $\text{[math]}$ ，则该圆锥的母线长l为 $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2020九上·雁江期末) 如图，在△ABC中，点D、E分别在AB、AC上，∠ADE＝∠C ，如果AE＝4，△ADE的面积为5，四边形BCED的面积为15，那么AB的长为.

答案解析收藏纠错 + 选题
17. 已知边长为6 $\text{[math]}$ 的等边三角形 $\text{[math]}$ ，以 $\text{[math]}$ 为直径画半圆（如图），则阴影部分的面积是（结果保留 $\text{[math]}$ ）

答案解析收藏纠错 + 选题
18. (2020九上·南宁期末) 在矩形 $\text{[math]}$ 中， $\text{[math]}$ 点 $\text{[math]}$ 是 $\text{[math]}$ 边上的一个动点，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 与点 $\text{[math]}$ ，交射线 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值是

答案解析收藏纠错 + 选题

三、解答题

19. 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
20. 解方程： $\text{[math]}$ .

答案解析收藏纠错 + 选题
21. 如图，在平面直角坐标系中，已知 $\text{[math]}$ 三个顶点的坐标分别为 $\text{[math]}$ .
1. （1）画出 $\text{[math]}$ 绕点A顺时针旋转90°后得到的 $\text{[math]}$ .
2. （2）以原点O为位似中心，在所给表格画出将 $\text{[math]}$ 三条边放大为原来2倍后的 $\text{[math]}$ .若 $\text{[math]}$ ，写出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题

22. (2020·南宁模拟) 为了了解学生对“预防新型冠状病毒”知识的掌握情况，学校组织了一次线上知识培训，培训结束后进行测试，在全校2000名学生中，分别抽取了男生，女生各15份成绩，整理分析过程如下，请补充完整.

（收集数据）

15名男生测试成绩统计如下：（满分100分）78，90，99，93，92，95，94，100，90，85，86，95，75，88，90

15名女生测试成绩统计如下：（满分100分）77，82，83，86，90，90，92，91，93，92，92，92，92，98，100

（整理、描述数据）

	70.5～75.5	75.5～80.5	80.5～85.5	85.5～90.5	90.5～95.5	95.5～100.5
男生	1	1	1	5	5	2
女生	0	1	2	3	7	2

（分析数据）

（1）两组样本数据的平均数、众数、中位数、方差如下表所示：

性别	平均数	众数	中位数	方差
男生	90	90	90	44.9
女生	90	$\text{[math]}$	$\text{[math]}$	32.8

在表中： $\text{[math]}$ . $\text{[math]}$ ；

（2）若规定得分在80分以上（不含80分）为合格，请估计全校学生中“预防新型冠状病毒”知识测试合格的学生有多少人？
（3）通过数据分析得到的结论，你认为男生和女生中谁的成绩比较好？请说明理由.

答案解析收藏纠错 + 选题

23. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上的中线，点E是 $\text{[math]}$ 的中点，过点A作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于F，连接 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是菱形.
答案解析收藏纠错 + 选题
24. 某商场准备采购一批特色商品，经调查，用5000元采购 $\text{[math]}$ 型商品的件数是用2000元采购 $\text{[math]}$ 型商品的件数的2倍，一件 $\text{[math]}$ 型商品的进价比一件 $\text{[math]}$ 型商品的进价多10元.
1. （1）求一件 $\text{[math]}$ ， $\text{[math]}$ 型商品的进价分别为多少元？
2. （2）若该商场购进 $\text{[math]}$ ， $\text{[math]}$ 型商品共200件进行试销，其中 $\text{[math]}$ 型商品的件数不大于 $\text{[math]}$ 型商品的件数，且不小于80件.已知 $\text{[math]}$ 型商品的售价为80元/件， $\text{[math]}$ 型商品的售价为60元/件，且 $\text{[math]}$ ， $\text{[math]}$ 型商品均全部售出.设购进 $\text{[math]}$ 型商品 $\text{[math]}$ 件，求该商场销售完这批商品的利润 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式，并写出 $\text{[math]}$ 的取值范围；
3. （3）在（2）的条件下，商场决定在试销活动中每售出一件 $\text{[math]}$ 型商品，就从一件 $\text{[math]}$ 型商品的利润中捐献慈善资金 $\text{[math]}$ 元 $\text{[math]}$ ，若该商场售完 $\text{[math]}$ 、 $\text{[math]}$ 型所有商品并捐献资金后获得的最大收益是4800元，求出 $\text{[math]}$ 值.
答案解析收藏纠错 + 选题
25. (2018·通辽) 如图，⊙O是△ABC的外接圆，点O在BC边上，∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线与AC的延长线相交于点P．
1. （1）求证：PD是⊙O的切线；
2. （2）求证：△ABD∽△DCP；
3. （3）当AB=5cm，AC=12cm时，求线段PC的长．
答案解析收藏纠错 + 选题
26. (2017·青海)
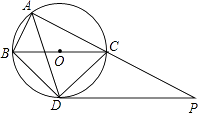
如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA=4，OC=3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交BE于点F，点D，E的坐标分别为（3，0），（0，1）．
1. （1）求抛物线的解析式；
2. （2）猜想△EDB的形状并加以证明；
3. （3）点M在对称轴右侧的抛物线上，点N在x轴上，请问是否存在以点A，F，M，N为顶点的四边形是平行四边形？若存在，请求出所有符合条件的点M的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题