20.
(2020高三上·菏泽期末)
中国提出共建“一带一路”,旨在促进更多的经济增长和更大的互联互通,随着“一带一路”的发展,中亚面粉、波兰苹果、法国红酒走上了国人的餐桌,中国制造的汽车、电子元件、农产品丰富着海外市场.为拓展海外市场,某电子公司新开发一款电子产品,该电子产品的一个系统

有3个电子元件组成,各个电子元件能正常工作的概率为

,且每个电子元件能否正常工作相互独立,若系统

中有超过一半的电子元件正常工作,则

可以正常工作,否则就需要维修,且维修所需费用为900元.

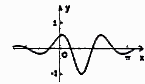 B .
B . 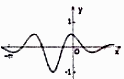 C .
C . 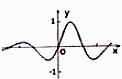 D .
D . 

