 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C . 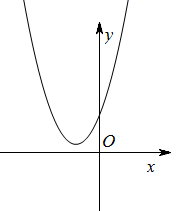 D .
D . 


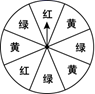
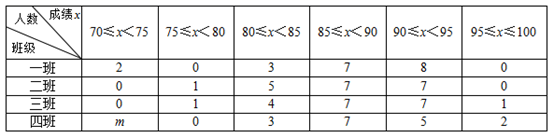
下面有四个推断:
①当摸球次数是300时,记录“摸到红球”的次数是99,所以“摸到红球”的概率是0.33;
②随着试验次数的增加,“摸到红球”的频率总在0.35附近摆动,显示出一定的稳定性,可以估计“摸到红球”的概率是0.35;
③可以根据本次实验结果,计算出盒子中约有红球7个;
④若再次开展上述摸球活动,则当摸球次数为500时,“摸到红球”的频率一定是0.40
所有合理推断的序号是.

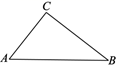
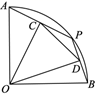
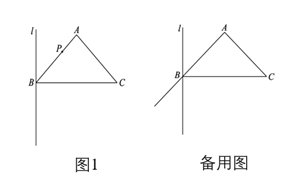
求作:∠CPB=∠A,使得顶点P在AB的垂直平分线上.
作法:①作AB的垂直平分线l,交AB于点O;
②以O为圆心,OA为半径画圆,⊙O与直线l的一个交点为P(点P与点C在AB的两侧);
③连接BP,CP.∠CPB就是所求作的角.
证明:连接OC,
∵l为AB的垂直平分线
∴OA=.
∵∠ACB=90°,
∴OA=OB=OC.
∴点A,B,C都在⊙O上.
又∵点P在⊙O上,
∴∠CPB=∠A()(填推理依据).
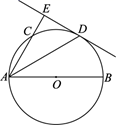

①求证:∠BDP =∠PCB;
②用等式表示线段BC,BD,BP之间的数量关系,并证明.
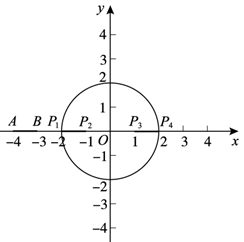
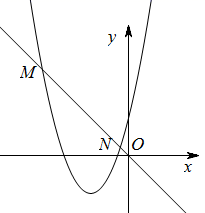
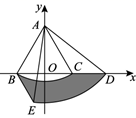
①当点B为(-3,0),如图所示,平移线段AB,在点P1(-2,0),P2(-1,0),P3(1,0),P4(2,0)中,连接点A与点 的线段的长度为d(AB,⊙O);
②当点B为(-4,1),求线段AB到⊙O的“极大距离”所对应的点A´的坐标:;