 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 




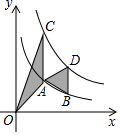

①若 面积最大时,求点
的坐标及
面积的最大值;
②在 轴上是否存在一点
,使得以
为顶点的四边形是平行四边形?如果存在,请直接写出点
的坐标;如果不存在,请说明理由.