河北省唐山市玉田县2020年中考数学二模试卷

更新时间：2024-11-06 浏览次数：193 类型：中考模拟

一、单选题

1. (2020·玉田模拟) 在－2，－1，0，1这四个数中，最小的数是（）

A . 0 B . －1 C . －2 D . 1

答案解析收藏纠错 + 选题
2. (2020·玉田模拟) 在“新冠”疫情期间，成都数字学校开设了语文、数学、英语等36个科目的网络直播课，四川省有1500万人次观看了课程．将数据“1500万”用科学记数法可表示为（）

A . 1.5×10⁶ B . 1.5×10⁷ C . 15×10⁶ D . 0.15×10⁸

答案解析收藏纠错 + 选题
3. (2020·玉田模拟) 如图，直线a∥b，∠1＝50°，∠2＝40°，则∠3的度数为（）

A . 40° B . 90° C . 50° D . 100°

答案解析收藏纠错 + 选题
4. (2020·玉田模拟) 如图一个五边形木架，要保证它不变形，至少要再钉上几根木条（）

A . 4 B . 3 C . 2 D . 1

答案解析收藏纠错 + 选题
5. (2024八上·肇源月考) 估计 $\text{[math]}$ 的值在（）

A . 2和3之间 B . 3和4之间 C . 4和5之间 D . 5和6之间

答案解析收藏纠错 + 选题
6. (2020·玉田模拟) 某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原正方体中，与“抗”字所在面相对的面上的汉字是（）

A . 一 B . 定 C . 胜 D . 利

答案解析收藏纠错 + 选题
7. (2020·玉田模拟) 下列“数字图形”中，既是轴对称图形，又是中心对称图形的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
8. (2020·玉田模拟) 如图是一个 $\text{[math]}$ 的方阵，其中每行、每列的两数和相等，则 $\text{[math]}$ 可以是（）

A . $\text{[math]}$ B . -1 C . 0 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024九下·广安期中) 下列说法正确的是（）

A . 了解我市市民知晓“礼让行人”交通新规的情况，适合全面调查 B . 甲、乙两人跳远成绩的方差分别为S_甲²=3，S_乙²=4，说明乙的跳远成绩比甲稳定 C . 一组数据2，2，3，4的众数是2，中位数是2.5 D . 可能性是1%的事件在一次试验中一定不会发生

答案解析收藏纠错 + 选题
10. (2020·玉田模拟) 关于x的一元二次方程x²﹣（k+3）x+2k+2＝0的根的情况，下面判断正确的是（　　）

A . 有两个相等的实数根 B . 有两个不相等的实数根 C . 有两个实数根 D . 无实数根

答案解析收藏纠错 + 选题
11. (2020·玉田模拟) 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ ．以点 $\text{[math]}$ 为圆心，以任意长为半径作弧分别交 $\text{[math]}$ 、 $\text{[math]}$ 于点 $\text{[math]}$ 、 $\text{[math]}$ ，再分别以点 $\text{[math]}$ 、 $\text{[math]}$ 为圆心，以大于 $\text{[math]}$ 的长为半径作弧交于点 $\text{[math]}$ ，作射线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则矩形 $\text{[math]}$ 的面积等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2020·玉田模拟) 如图，在直角坐标系中，已知菱形 $\text{[math]}$ 的顶点 $\text{[math]}$ ， $\text{[math]}$ ．作菱形 $\text{[math]}$ 关于 $\text{[math]}$ 轴的对称图形 $\text{[math]}$ ，再作图形 $\text{[math]}$ 关于点 $\text{[math]}$ 的中心对称图形 $\text{[math]}$ ，则点 $\text{[math]}$ 的对应点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2023九上·宁明月考) 在平面直角坐标系中，抛物线 $\text{[math]}$ 经过变换后得到抛物线 $\text{[math]}$ ，则这个变换可以是（）

A . 向左平移2个单位 B . 向右平移2个单位 C . 向左平移8个单位 D . 向右平移8个单位

答案解析收藏纠错 + 选题
14. 在如图所示的象棋盘（各个小正方形的边长均相等）中，根据“马走日”的规则，“马”应落在下列哪个位置处，能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”，“兵”所在位置的格点构成的三角形相似（）

A . ①处 B . ②处 C . ③处 D . ④处

答案解析收藏纠错 + 选题
15. (2021八下·海拉尔期末) 如图，正方形 $\text{[math]}$ 的边长为4，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿 $\text{[math]}$ 移动至终点 $\text{[math]}$ ，设 $\text{[math]}$ 点经过的路径长为x， $\text{[math]}$ 的面积为y，则下列图象能大致反映y与x函数关系的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
16. (2020七上·建昌期末) 如图，数轴上 $\text{[math]}$ 、 $\text{[math]}$ 两点的距离为4，一动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，按以下规律跳动：第1次跳动到 $\text{[math]}$ 的中点 $\text{[math]}$ 处，第2次从 $\text{[math]}$ 点跳动到 $\text{[math]}$ 的中点 $\text{[math]}$ 处，第3次从 $\text{[math]}$ 点跳动到 $\text{[math]}$ 的中点 $\text{[math]}$ 处，按照这样的规律继续跳动到点 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ 是整数）处，问经过这样2020次跳动后的点与 $\text{[math]}$ 点的距离是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

17. (2020·玉田模拟) 若n﹣2与n+4互为相反数，则n的值为．

答案解析收藏纠错 + 选题
18. (2020·玉田模拟) 某体育看台侧面的示意图如图所示，观众区 $\text{[math]}$ 的坡度 $\text{[math]}$ 为 $\text{[math]}$ ，顶端 $\text{[math]}$ 离水平地面 $\text{[math]}$ 的高度为 $\text{[math]}$ ，从顶棚的 $\text{[math]}$ 处看 $\text{[math]}$ 处的仰角 $\text{[math]}$ ，竖直的立杆上 $\text{[math]}$ 、 $\text{[math]}$ 两点间的距离为 $\text{[math]}$ ， $\text{[math]}$ 处到观众区底端 $\text{[math]}$ 处的水平距离 $\text{[math]}$ 为 $\text{[math]}$ ．则观众区的水平宽度 $\text{[math]}$ $\text{[math]}$ ；顶棚的 $\text{[math]}$ 处离地面的高度 $\text{[math]}$ $\text{[math]}$ ．（ $\text{[math]}$ ， $\text{[math]}$ ，结果精确到 $\text{[math]}$ ）

答案解析收藏纠错 + 选题
19. (2020·玉田模拟) 有三个大小一样的正六边形，可按下列方式进行拼接：
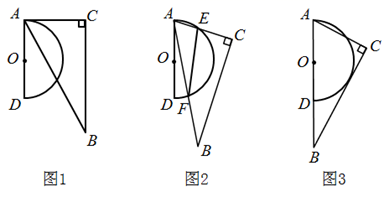
方式1：如图1；

方式2：如图2；

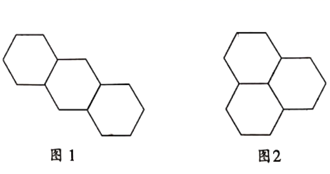
若有四个边长均为1的正六边形，采用方式1拼接，所得图案的外轮廓的周长是.有 $\text{[math]}$ 个边长均为1的正六边形，采用上述两种方式的一种或两种方式混合拼接，若得图案的外轮廓的周长为18，则n的最大值为．

答案解析收藏纠错 + 选题

三、解答题

20. (2020·玉田模拟) 先化简，再求值： $\text{[math]}$ 其中 $\text{[math]}$ 的值从不等式组 $\text{[math]}$ 的整数解中选取．

答案解析收藏纠错 + 选题

21. (2024·茅箭模拟) 为了庆祝中华人民共和国成立70周年，某市决定开展“我和祖国共成长”主题演讲比赛，某中学将参加本校选拔赛的40名选手的成绩(满分为100分，得分为正整数且无满分，最低为75分)分成五组，并绘制了下列不完整的统计图表.

分数段	频数	频率
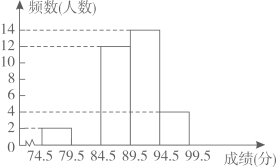
74.5～79.5	2	0.05
79.5～84.5	m	0.2
84.5～89.5	12	0.3
89.5～94.5	14	n
94.5～99.5	4	0.1

（1）表中m＝，n＝；
（2）请在图中补全频数直方图；
（3）甲同学的比赛成绩是40位参赛选手成绩的中位数，据此推测他的成绩落在分数段内；
（4）选拔赛中，成绩在94.5分以上的选手，男生和女生各占一半，学校从中随机确定2名选手参加全市决赛，请用列举法或树状图法求恰好是一名男生和一名女生的概率.

答案解析收藏纠错 + 选题

22. (2021·石家庄月考) 如图，认真观察下面这些算式，并结合你发现的规律，完成下列问题：
①3²﹣1²＝（3+1）（3﹣1）＝8＝8×1，

②5²﹣3²＝（5+3）（5﹣3）＝16＝8×2，

③7²﹣5²＝（7+5）（7﹣5）＝24＝8×3，

④9²﹣7²＝（9+7）（9﹣7）＝32＝8×4．

…
1. （1）请写出：
  算式⑤；
  
  算式⑥；
2. （2）上述算式的规律可以用文字概括为：“两个连续奇数的平方差能被8整除”，如果设两个连续奇数分别为2n﹣1和2n+1（n为整数），请说明这个规律是成立的；
3. （3）你认为“两个连续偶数的平方差能被8整除”这个说法是否也成立呢？请说明理由．
答案解析收藏纠错 + 选题
23. (2020·玉田模拟) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 边上一点，连接 $\text{[math]}$ ，将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 得到线段 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 延长线于点 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求线段 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 所形成的图形面积．
答案解析收藏纠错 + 选题
24. (2020·玉田模拟) 小明在妈妈的帮助下，利用社区提供的免费摊点卖玩具，已知小明所有玩具的进价均2元/个．在销售过程中发现：每天玩具销售量 $\text{[math]}$ （件）与销售价格 $\text{[math]}$ （元/件）的关系如图所示，其中 $\text{[math]}$ 段为反比例函数图象的一部分， $\text{[math]}$ 段为一次函数图象的一部分，设小明销售这种玩具的日利润为 $\text{[math]}$ 元．
1. （1）根据图象，求出 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式；
2. （2）求销售这种玩具的日利润 $\text{[math]}$ （元）与 $\text{[math]}$ （元/件）之间的函数关系式，并求每天利润的最大值．
答案解析收藏纠错 + 选题
25. (2020·玉田模拟) 将 $\text{[math]}$ 的顶点 $\text{[math]}$ 放在半圆 $\text{[math]}$ 上，现从 $\text{[math]}$ 与半圆 $\text{[math]}$ 相切于点 $\text{[math]}$ （如图1）的位置开始，将 $\text{[math]}$ 绕着点 $\text{[math]}$ 顺时针旋转，设旋转角为 $\text{[math]}$ ，旋转后 $\text{[math]}$ 、 $\text{[math]}$ 分别与半圆 $\text{[math]}$ 交于点 $\text{[math]}$ 、 $\text{[math]}$ ，连接 $\text{[math]}$ （如图2）．已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，半圆 $\text{[math]}$ 的直径为8．
1. （1）求图2中 $\text{[math]}$ 的长；
2. （2） $\text{[math]}$ 绕着点 $\text{[math]}$ 顺时针旋转到如图3位置时， $\text{[math]}$ $\text{[math]}$ ，此时边 $\text{[math]}$ 与⊙O的位置关系是什么？并说明理由；
3. （3）请直接写出在旋转的过程中，点 $\text{[math]}$ 到 $\text{[math]}$ 的距离 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
26. (2020·玉田模拟) 如图1，二次函数 $\text{[math]}$ 的图象过原点，与 $\text{[math]}$ 轴的另一个交点为 $\text{[math]}$ ．
1. （1）求该二次函数的解析式；
2. （2）如图2， $\text{[math]}$ 与二次函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ，求 $\text{[math]}$ 的面积；
3. （3）如图3，直线 $\text{[math]}$ 与二次函数 $\text{[math]}$ 的图象交于 $\text{[math]}$ 、 $\text{[math]}$ 两点（点 $\text{[math]}$ 在点 $\text{[math]}$ 的左侧），过 $\text{[math]}$ 、 $\text{[math]}$ 两点分别作 $\text{[math]}$ 轴的垂线，垂足分别为点 $\text{[math]}$ 、点 $\text{[math]}$ ．判断四边形 $\text{[math]}$ 的形状，并说明理由；
4. （4）如图4，在（3）的条件下，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发沿射线 $\text{[math]}$ 以每秒1个单位长度匀速运动，同时动点 $\text{[math]}$ 以相同的速度从点 $\text{[math]}$ 出发沿线段 $\text{[math]}$ 匀速运动，到达点 $\text{[math]}$ 时立即原速返回，当动点 $\text{[math]}$ 返回到点 $\text{[math]}$ 时， $\text{[math]}$ 、 $\text{[math]}$ 两点同时停止运动，设运动时间为 $\text{[math]}$ 秒（ $\text{[math]}$ ）．过点 $\text{[math]}$ 向 $\text{[math]}$ 轴作垂线，交抛物线于点 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，问：以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 四点为顶点构成的四边形能否是平行四边形？若能，请直接写出 $\text{[math]}$ 的值；若不能，请说明理由．
答案解析收藏纠错 + 选题