江西省宜春高安市2020年中考数学二模试卷

更新时间：2024-11-06 浏览次数：228 类型：中考模拟

一、单选题

1. (2020·高安模拟) 下列四个数中，最小的一个数是（　　）

A . 0 B . －2020 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·高安模拟) 不等式组 $\text{[math]}$ 的所有整数解的积为（　　）

A . 0 B . 1 C . －1 D . 2

答案解析收藏纠错 + 选题
3. (2020·高安模拟) 将图（1）的正方体用阴影部分所在的平面切割后，剩下如图（2）所示的几何体，则该几何体的俯视图为（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2021七上·高青期中) 如图，AB＝AC，若要使△ABE≌△ACD，则添加的一个条件不能是（）

A . ∠B＝∠C B . BE＝CD C . BD＝CE D . ∠ADC＝∠AEB

答案解析收藏纠错 + 选题
5. (2024九下·高安期中) 若关于x的一元二次方程 $\text{[math]}$ 有两个实数根 $\text{[math]}$ ， $\text{[math]}$ ，则下列说法正确的是（　　）

A . a的值可以是0 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$ 都是正数

答案解析收藏纠错 + 选题
6. (2020·高安模拟) 二次函数y=﹣x²+mx的图象如图，对称轴为直线x=2，若关于x的一元二次方程﹣x²+mx﹣t=0（t为实数）在1＜x＜5的范围内有解，则t的取值范围是（）

A . t＞﹣5 B . ﹣5＜t＜3 C . 3＜t≤4 D . ﹣5＜t≤4

答案解析收藏纠错 + 选题

二、填空题

7. (2024九下·闵行月考) 若式子 $\text{[math]}$ 有意义，则x的取值范围是

答案解析收藏纠错 + 选题
8. (2020·高安模拟) 2019年是高安发展史上进位赶超、值得铭记的一年．全年实现生产总值448.78亿元，同比净增29.78亿元．“十全十美、品牌高安”建设迈出更加坚实步伐．数据448.78亿用科学记数法表示为．

答案解析收藏纠错 + 选题
9. (2020·高安模拟) 程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．根据如图所示的计算程序，若输入的值x＝2020，则输出的值为．

答案解析收藏纠错 + 选题
10. (2022九上·寻乌期末) 已知圆锥的母线长为10，侧面积为 $\text{[math]}$ ，则其侧面展开图的圆心角度数为度．

答案解析收藏纠错 + 选题
11. (2020·高安模拟) 如图，两张等宽的纸条交叉叠放在一起，若重叠都分构成的四边形ABCD中，AB=3，BD=4．则AC的长为．

答案解析收藏纠错 + 选题
12. (2020·高安模拟) 如图，已知⊙P的半径是1，圆心P在抛物线y＝ $\text{[math]}$ -x- $\text{[math]}$ 上运动，当⊙P与x轴相切时，圆心P的坐标为．

答案解析收藏纠错 + 选题

三、解答题

13. (2020·高安模拟)
1. （1）计算： $\text{[math]}$
2. （2）如图，直线AB∥CD，MN⊥CE于M点，若∠MNC＝60°，求∠EMB的度数．
答案解析收藏纠错 + 选题
14. (2020·高安模拟) 先化简：（ $\text{[math]}$ +1）÷ $\text{[math]}$ ，再从﹣2≤a≤2中选取一个合适的整数代入求值．

答案解析收藏纠错 + 选题
15. (2020·高安模拟) 如图，在5×5的正方形网格中， $\text{[math]}$ 的顶点都是格点（小正方形的顶点），且点D是AB边的中点．请仅用无刻度的直尺分别按下列要求画图（不写画法，保留画图痕迹）．

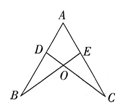
（1）如图1，在AC边上找点E，使 $\text{[math]}$ 与 $\text{[math]}$ 相似；
（2）如图2，在BC边上找点F，使 $\text{[math]}$ 与 $\text{[math]}$ 相似．

答案解析收藏纠错 + 选题
16. (2020·高安模拟) 保护环境卫生，垃圾分类开始实施．我市为了促进生活垃圾的分类处理，将生活垃圾分为“可回收物”、“有害垃圾”、“湿垃圾”、“干垃圾”四类，并且设置了相应的垃圾箱．
1. （1）小亮将妈妈分类好的某类垃圾随机投入到四种垃圾箱某类箱内，请写出小亮投放正确的概率为；
2. （2）经过妈妈的教育，小明已经分清了“有害垃圾”，但仍然分不清“可回收物”、“湿垃圾”和“干垃圾”，这天小亮要将妈妈分类好的四类垃圾投入到四种垃圾箱内，请求出小明投放正确的概率；
3. （3）请你就小亮投放垃圾的事件提出两条合理化建议．
答案解析收藏纠错 + 选题
17. (2020·高安模拟) 定义：对于函数y ，我们称函数|y|叫做函数y的正值函数．例如：函数y＝ $\text{[math]}$ 的正值函数为y＝| $\text{[math]}$ |．如图为曲线y＝ $\text{[math]}$ （x＞0）．
1. （1）请你在图中画出y＝x+3的正值函数的图象并写出y＝x+3的正值函数的两条性质；
2. （2）设y＝x+3的正值函数的图象与x轴、y轴、曲线y＝ $\text{[math]}$ （x＞0）的交点分别是A ， B ， C．点D是线段AC上一动点（不包括端点），过点D作x轴的平行线，与正值函数图象交于另一点E，与曲线交于点P．试求△PAD的面积的最大值；
答案解析收藏纠错 + 选题

18. (2020八下·高安期末) 为宣传普及新冠肺炎防治知识，引导学生做好防控．某校举行了主题为“防控新冠，从我做起”的线上知识竞赛活动，测试内容为20道判断题，每道题5分，满分100分，为了解八、九年级学生此次竞赛成绩的情况，分别随机在八、九年级各抽取了20名参赛学生的成绩．已知抽查得到的八年级的数据如下：80，95，75，75，90，75，80，65，80，85，75，65，70，65，85，70，95，80，75，80．

为了便于分析数据，统计员对八年级数据进行了整理，得到了表一：

成绩等级	分数（单位：分）	学生数
D等	60＜x≤70	5
C等	70＜x≤80	a
B等	80＜x≤90	b
A等	90＜x≤100	2

九年级成绩的平均数、中位数、优秀率如下：（分数80分以上、不含80分为优秀）

年级	平均数	中位数	优秀率
八年级	77.5	c	m%
九年级	76	82.5	50%

（1）根据题目信息填空：a＝，c＝，m＝；
（2）八年级小宇和九年级小乐的分数都为80分，请判断小宇、小乐在各自年级的排名哪位更靠前？请简述你的理由；
（3）若九年级共有600人参加参赛，请估计九年级80分以上的人数．

答案解析收藏纠错 + 选题

19. (2020·高安模拟) 如图1，是一款常见的海绵拖把，图2是其平面示意图，EH是拖把把手，F是把手的一个固定点，海绵安装在两片活动骨架PA，PB上，骨架的端点P只能在线段FH上移动，当海绵完全张开时，PA，PB分别与HMHN重合；当海绵闭合时，PA，PB与FH重合．已知直杆EH=120cm，FH=20cm．(参考数据：sin13°≈0.225，cos13°≈0.974，tan13°≈0.231，π取3.14)
1. （1）若∠APB=90°，求EP的长(结果保留根号)
2. （2）若∠APB=26°，求MA的长(结果保留小数点后一位)
3. （3）海绵从完全张开到闭合的过程中，直接写出PA的中点Q运动的路径长．
答案解析收藏纠错 + 选题

20. (2020·高安模拟) 如图，半圆O的直径AB＝5cm，点C是半圆O上的动点，连结AC、BC．设AC＝x（单位：cm），△ABC的面积为y（单位：cm2，当点C与A、B重合时，y的值为0）．轩轩根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．

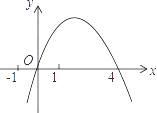
下面是轩轩的探究过程，请补充完整：

（1）按照下表中自变量x的值进行取点、画图、测量，分别得到了x与y的几组值，结果如表：

x/cm	0	0.5	1	1.5	2	2.5	3	3.5	4	4.5	5
y/cm²	0	1.25	2.45	3.58	4.57	5.41		6.25		4.91	0

该函数的表达式为，自变量x的取值范围为．

（2）在右图中建立平面直角坐标系，描出以补全后的表中各组对应值为坐标的点，画出该函数的图象．
（3）结合画出的函数图象，解决问题：在（2）问的直角坐标系中画出直线y₁＝x，根据图象得出当y＝y₁时x的正数值约为（精确到0.1）

答案解析收藏纠错 + 选题

21. (2020·高安模拟) 如图，在△ABC中，AB＝AC，以边AB为直径的⊙O交边BC于点D，交边AC于点E．过D点作DF⊥AC于点F．
1. （1）求证：DF是⊙O的切线；
2. （2）求证：CF＝EF；
3. （3）延长FD交边AB的延长线于点G，若EF＝3，BG＝9时，求⊙O的半径．
答案解析收藏纠错 + 选题
22. (2020·高安模拟) 定义：我们把对角线互相垂直的四边形叫做神奇四边形．顺次连接四边形各边中点得到的四边形叫做中点四边形．
1. （1）判断：
  ①在平行四边形、矩形、菱形中，一定是神奇四边形的是；
  
  ②命题：如图1，在四边形 $\text{[math]}$ 中， $\text{[math]}$ 则四边形 $\text{[math]}$ 是神奇四边形．此命题是（填“真”或“假”)命题；
  
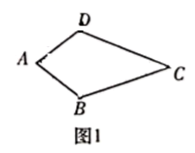
  ③神奇四边形的中点四边形是
2. （2）如图2，分别以 $\text{[math]}$ 的直角边 $\text{[math]}$ 和斜边 $\text{[math]}$ 为边向外作正方形 $\text{[math]}$ 和正方形 $\text{[math]}$ ，连接 $\text{[math]}$
  
  ①求证：四边形 $\text{[math]}$ 是神奇四边形；
  
  ②若 $\text{[math]}$ ，求 $\text{[math]}$ 的长；
3. （3）如图3，四边形 $\text{[math]}$ 是神奇四边形，若 $\text{[math]}$ 分别是方程 $\text{[math]}$ 的两根，求k的值．
答案解析收藏纠错 + 选题
23. (2020·高安模拟) 已知点P为抛物线y $\text{[math]}$ x²上一动点，以P为顶点，且经过原点O的抛物线，记作“y_p”，设其与x轴另一交点为A ，点P的横坐标为m ．
1. （1） ①当△OPA为直角三角形时，m=　　 ▲　　；
  ②当△OPA为等边三角形时，求此时“y_p”的解析式；
2. （2）若P点的横坐标分别为1，2，3，…n(n为正整数)时，抛物线“y_p”分别记作“ $\text{[math]}$ ”、“ $\text{[math]}$ ”…，“ $\text{[math]}$ ”，设其与x轴另外一交点分别为A₁ ， A₂ ， A₃ ， …A_n ，过P₁ ， P₂ ， P₃ ， …P_n作x轴的垂线，垂足分别为H₁ ， H₂ ， H₃ ， …H_n ．
  　1)① P_n的坐标为；OA_n=；(用含n的代数式来表示)
  
  ②当P_nH_n﹣OA_n=16时，求n的值．
  
  　2)是否存在这样的A_n ，使得∠OP₄A_n=90°，若存在，求n的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题