初中数学浙教版八年级下册第四章平行四边形强化提升训练

更新时间：2021-04-20 浏览次数：283 类型：单元试卷

一、单选题

1. (2019八上·涧西月考) 如图，∠A+∠B+∠C+∠D+∠E+∠F的度数为（）

A . 180° B . 360 C . 270° D . 540°

答案解析收藏纠错 + 选题
2. (2020九上·宽城期末) 如图，在边长为1的正六边形 $\text{[math]}$ 中，M是边 $\text{[math]}$ 上一点，则线段 $\text{[math]}$ 的长可以是（）

A . 1.4 B . 1.6 C . 1.8 D . 2.2

答案解析收藏纠错 + 选题
3. (2017八下·无棣期末)
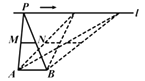
如图，点A，B为定点，定直线l//AB，P是l上一动点．点M，N分别为PA，PB的中点，对于下列各值：①线段MN的长；②△PMN的面积；③△PAB的周长；④∠APB的大小；⑤直线MN，AB之间的距离．其中会随点P的移动而不改变的是（）

A . ①②③ B . ①②⑤ C . ②③④ D . ②④⑤

答案解析收藏纠错 + 选题
4. 如图所示的方格纸上有一平行四边形ABCD，其顶点均在网格线的交点上，且E点在AD上．今大华在方格纸网格线的交点上任取一点F，发现△FBC的面积比△EBC的面积大．判断下列哪一个图形可表示大华所取F点的位置？（　　　）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2020·青山模拟) 如图，点O是 $\text{[math]}$ 的对称中心， $\text{[math]}$ ，E、F是 $\text{[math]}$ 边上的点，且 $\text{[math]}$ ；G、H是 $\text{[math]}$ 边上的点，且 $\text{[math]}$ ，若 $\text{[math]}$ 分别表示 $\text{[math]}$ 和 $\text{[math]}$ 的面积，则 $\text{[math]}$ 与 $\text{[math]}$ 之间的等量关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020·青山模拟) 如图，已知 $\text{[math]}$ ABCD三个顶点坐标是A(-1，0) 、B(-2，-3) 、C(2，-1) ，那么第四个顶点D的坐标是（）

A . (3，1) B . (3，2) C . (3，3) D . (3，4)

答案解析收藏纠错 + 选题
7. (2020七下·淮阳期末) 如图所示，已知△ABC与△CDA关于点O对称，过O作EF分别交AD，BC于点E，F，下面的结论：①点E和点F，点B和点D是关于点O的对应点；②直线BD必经过点O；③四边形ABCD是中心对称图形；④四边形DEOC与四边形BFOA的面积必相等；⑤△AOE与△COF成中心对称，其中正确的有（）

A . 1个 B . 2个 C . 3个 D . 5个

答案解析收藏纠错 + 选题
8. (2020九下·青县开学考) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，E是 $\text{[math]}$ 的中点．点P以每秒1个单位长度的速度从点A出发，沿 $\text{[math]}$ 向点D运动；点Q同时以每秒3个单位长度的速度从点C出发，沿 $\text{[math]}$ 向点B运动．点P停止运动时，点Q也随之停止运动．若以点 $\text{[math]}$ 为顶点的四边形是平行四边形，则点P运动的时间为（）

A . 1 B . $\text{[math]}$ C . 2或 $\text{[math]}$ D . 1或 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022八下·抚州期末) 如图，在平行四边形ABCD中，对角线AC，BD交于点O，BD＝2AD，E，F，G分别是OA，OB，CD的中点，EG交FD于点H．则下列结论：①ED⊥CA；②EF＝CG；③EH= $\text{[math]}$ EG；④S_△EFD＝S_△CEG成立的个数有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
10. (2020八上·宽城期末) 用反证法证明“在三角形中，至少有一个内角大于或等于60°”时，应先假设（）

A . 在三角形中，三个内角都大于60° B . 在三角形中，三个内角都小于60° C . 在三角形中，至少有一个内角大于60° D . 在三角形中，至少有一个内角小于60°

答案解析收藏纠错 + 选题

二、填空题

11. (2024八上·富裕月考) 过四边形的一个顶点可以画一条对角线，且把四边形分成两个三角形；过五边形的一个顶点可以画两条对角线，且把五边形分成三个三角形；......猜想：过n边形的一个顶点可以画条对角线，且把n边形分成个三角形.

答案解析收藏纠错 + 选题
12. (2020八下·东丽期末) 在 $\text{[math]}$ 中， $\text{[math]}$ 边上的高为4， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的周长等于.

答案解析收藏纠错 + 选题
13. (2019·新宁模拟) 如图，在平面直角坐标系中，△ABC的顶点A在第一象限，点B，C的坐标为（2，1），（6，1），∠BAC=90°，AB=AC，直线AB交x轴于点P．若△ABC与△A'B'C'关于点P成中心对称，则点A'的坐标为．

答案解析收藏纠错 + 选题
14. (2020八下·惠州期末) 如图四边形ABCD ， AD∥BC ， AB⊥BC ， AD＝1，AB＝2，BC＝3，P为AB边上的一动点，以PD ， PC为边作平行四边形PCQD ，则对角线PQ的长的最小值是.

答案解析收藏纠错 + 选题
15. (2021八上·南浔期末) 如图所示的三角形纸片中， $\text{[math]}$ ， BC=12cm， $\text{[math]}$ ，折叠这个三角形，使点B落在AC的中点D处，折痕为EF，那么BF的长为cm.

答案解析收藏纠错 + 选题
16. (2019七下·北京期末) 用一个值a说明命题“若ax＞a，则x＞1”是不正确的，则a的值可以是．

答案解析收藏纠错 + 选题

三、综合题

17. 设a，b，c是不全相等的任意整数，若x＝a²－bc，y＝b²－ac，z＝c²－ab.求证：x，y，z中至少有一个大于零．

答案解析收藏纠错 + 选题
18. (2020八下·海州期末) 如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后， $\text{[math]}$ 的顶点均在格点上，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ .

（ 1 ）把 $\text{[math]}$ 向上平移6个单位后得到对应的 $\text{[math]}$ ，画出 $\text{[math]}$ ，并写出 $\text{[math]}$ 的坐标；

（ 2 ）以原点 $\text{[math]}$ 为对称中心，画出 $\text{[math]}$ 关于原点对称的 $\text{[math]}$ ，并写出点 $\text{[math]}$ 的坐标；

（ 3 ） $\text{[math]}$ 与 $\text{[math]}$ 是否为中心对称，如果是，请直接写出对称中心坐标：如果不是，请说明理由.

答案解析收藏纠错 + 选题
19. (2020八下·长沙期中) 如图，在平面直角坐标系中，矩形OABC的三个顶点A，O，C在坐标轴上，矩形的面积为12，对角线AC所在直线的解析式为y＝kx－4k（k≠0）．
1. （1）求A，C的坐标；
2. （2）若D为AC中点，过D的直线交y轴负半轴于E，交BC于F，且OE＝1，求直线EF的解析式；
3. （3）在（2）的条件下，在坐标平面内是否存在一点G，使以C，D，F，G为顶点的四边形为平行四边形，若存在，请直接写出点G的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
20. (2020八上·包河期中) 在活动课上我们曾经探究过三角形内角和等于180°，四边形内角和等于360°，五边形内角和等于540°，…，请同学们仔细读题，看图，解决下面的问题：
1. （1）如图①，△OAB、△OCD的顶点O重合，且∠A+∠B+∠C+∠D＝180°，则∠AOB+∠COD＝（直接写出结果）．
2. （2）连接AD、BC，若AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线．
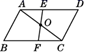
  ①如图②，如果∠AOB＝110°，求∠COD的度数．
  
  ②如图③，若∠AOD＝∠BOC，AB与CD平行吗？请写出理由．
答案解析收藏纠错 + 选题
21. (2020八下·兴城期末) 如图，在平面直角坐标系中，一次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与正比例函数 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ .
1. （1）求此一次函数的解析式；
2. （2）求出 $\text{[math]}$ 的面积；
3. （3）点 $\text{[math]}$ 在此坐标平面内，且知以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点四边形是平行四边形，请直接写出符合条件的点 $\text{[math]}$ 的坐标.
答案解析收藏纠错 + 选题
22. (2019七下·如皋期中) △ABC在平面直角坐标系中如图所示，
1. （1） S_△ABC＝．
2. （2） x轴上是否存在点P，使得S_△BCP＝2S_△ABC ，若不存在，说明理由；若存在，求出P点的坐标．
3. （3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．
答案解析收藏纠错 + 选题
23. (2019八下·成都期末) 已知：点A、C分别是∠B的两条边上的点，点D、E分别是直线BA、BC上的点，直线AE、CD相交于点P．
1. （1）点D、E分别在线段BA、BC上；
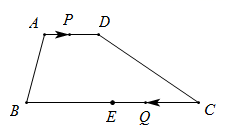
  ①若∠B＝60°（如图1），且AD＝BE，BD＝CE，求∠APD的度数；
  
  ②若∠B＝90°（如图2），且AD＝BC，BD＝CE，求∠APD的度数；
2. （2）如图3，点D、E分别在线段AB、BC的延长线上，若∠B＝90°，AD＝BC，∠APD＝45°，求证：BD＝CE．
答案解析收藏纠错 + 选题
24. (2020八上·肇东期中) 已知点O是△ABC内任意一点，连接OA并延长到点E，使得AE＝OA，以OB，OC为邻边作平行四边形OBFC，连接OF，与BC交于点H，连接EF．
1. （1）问题发现：如图1，若△ABC为等边三角形，线段EF与BC的位置关系是，数量关系为；
2. （2）拓展探究：如图2，若△ABC为等腰直角三角形（BC为斜边），（1）中的两个结论是否成立？若成立，请给予证明；若不成立，请写出正确的结论再给予证明；
3. （3）解决问题：如图3，若△ABC是等腰三角形，AB＝AC＝5，BC＝6，请你直接写出线段EF的长．
答案解析收藏纠错 + 选题