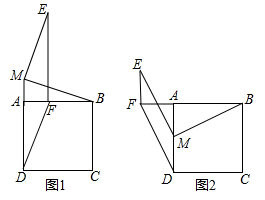
 B .
B .  C .
C . 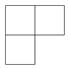 D .
D . 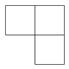
| 金额/元 | 5 | 10 | 20 | 50 | 100 |
| 人数 | 6 | 17 | 14 | 8 | 5 |
则他们捐款金额的平均数、中位数、众数分别是( )





| 时间x(天) | 1 | 30 | 60 | 90 |
| 每天销售量p(件) | 198 | 140 | 80 | 20 |