 B .
B .  C .
C . 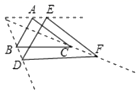 D .
D . 


|
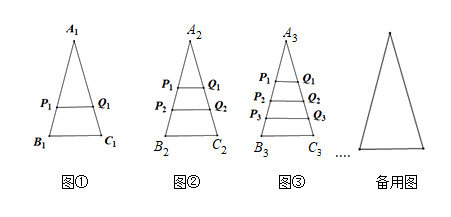
平均做家务时间(小时) |
0.5 |
1 |
1.5 |
2 |
2.5 |
|
人数 |
3 |
3 |
2 |
1 |
1 |


|
视力 |
频数(人) |
频率 |
|
4.0≤x<4.3 |
20 |
0.1 |
|
4.3≤x<4.6 |
40 |
0.2 |
|
4.6≤x<4.9 |
70 |
0.35 |
|
4.9≤x<5.2 |
a |
0.3 |
|
5.2≤x<5.5 |
10 |
b |


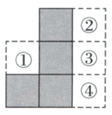
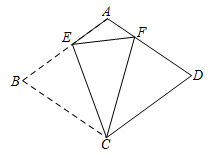
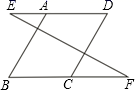
①如图2,在AB上找点P,使得AP:PB=1:3;
②如图3,在△ABC中内找一点G,连接GA、GB、GC,将△ABC分成面积相等的三部分;
③如图4,在△ABC中,AB与网格线的交点为D,画点E,使DE⊥AC.
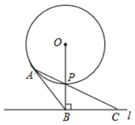

(问题背景)如图1,在△ABC中,点D在边BC上且满足∠BAD=∠ACB,求证:BA2=BD•BC;
(尝试应用)如图2,在△ABC中,点D在边BC上且满足∠BAD=∠ACB,点E在边AB上,点G在AB的延长线上,延长ED交CG于点F,若3AD=2AC,BE=ED,BG=2,DF=1,求BE的长度;
(拓展创新)如图3,在△ABC中,点D在边BC上(AB≠AD)且满足∠ACB=2∠BAD,DH⊥AB垂足为H,若 ,请直接写出
的值 ▲ .