北京市门头沟区2021年中考数学一模试卷

更新时间：2021-05-21 浏览次数：216 类型：中考模拟

一、单选题

1. (2021·厦门模拟) 如图，在 $\text{[math]}$ 中，BC边上的高是（）

A . CD B . AE C . AF D . AH

答案解析收藏纠错 + 选题
2. (2021·郑州模拟) 根据国家卫健委官网统计，截至2021年4月10日，31个省（自治区、直辖市）和新疆生产建设兵团累计报告接种新冠病毒疫苗16447.1万剂次，将16447.1万用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021·门头沟模拟) 下列图形中，既是轴对称图形又是中心对称图形的是（）

A . 等边三角形 B . 平行四边形 C . 等腰梯形圆 D . 圆

答案解析收藏纠错 + 选题
4. (2021七上·东莞月考) 某个几何体的展开图如图所示，该几何体是（）

A . 三棱柱 B . 三棱锥 C . 长方体 D . 圆柱

答案解析收藏纠错 + 选题
5. (2021·门头沟模拟) 内角和与外角和相等的多边形是（）

A . 六边形 B . 五边形 C . 四边形 D . 三角形

答案解析收藏纠错 + 选题
6. (2024七下·平果月考) 如图，直线AB ， CD交于点O ，射线OE平分 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021·厦门模拟) 点a ， b在数轴上的位置如图所示，且满足 $\text{[math]}$ ， $\text{[math]}$ ，则原点所在的位置有可能是（）

A . 点A B . 点B C . 点C D . 点D

答案解析收藏纠错 + 选题
8. (2021·门头沟模拟) 在物理实验室实验中，为了研究杠杆的平衡条件，设计了如下实验，如图，铁架台左侧钩码的个数与位置都不变，在保证杠杆水平平衡的条件下，右侧采取变动钩码数量即改变力F ，或调整钩码位置即改变力臂L ，确保杠杆水平平衡，则力F与力臂L满足的函数关系是（）

A . 正比例函数关系 B . 反比例函数关系 C . 一次函数关系 D . 二次函数关系

答案解析收藏纠错 + 选题

二、填空题

9. (2024八下·沙河口期末) 若 $\text{[math]}$ 在实数范围内有意义，则实数x的取值范围是.

答案解析收藏纠错 + 选题
10. (2021·门头沟模拟) 如图所示的网格是正方形网格，点A ， B ， C是网格线交点，那么 $\text{[math]}$ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2021七下·渝中期末) 请你写出一个大于2小于3的无理数是．

答案解析收藏纠错 + 选题
12. (2021·门头沟模拟) 已知 $\text{[math]}$ 且 $\text{[math]}$ ，写出一组符合条件的值．

答案解析收藏纠错 + 选题
13. (2021·门头沟模拟) 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个实数根，则k的取值范围是．

答案解析收藏纠错 + 选题
14. (2021·门头沟模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，半径 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2021·门头沟模拟) 下面是某小区随机抽取的100户家庭的月用电量情况统计表：

月户用电量x（千瓦时/户．月）

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

户数（户）

5

22

27

31

15

从中任意抽出一个家庭进行用电情况调查，则抽到的家庭月用电量为第二档（用电量大于240小于等于400为第二档）的概率为．

答案解析收藏纠错 + 选题

16. (2021·门头沟模拟) 以下是小亮的妈妈做晚饭的食材准备及加工时间列表，有一个炒菜锅，一个电饭煲，一个煲汤锅，两个燃气灶可用，做好这顿晚餐一般情况下至少需要分钟．

用时种类	准备时间（分钟）	加工时间（分钟）
米饭	3	30
炒菜1	5	6
炒菜2	5	8
汤	5	15

答案解析收藏纠错 + 选题

三、解答题

17. (2021·门头沟模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2021·建邺模拟) 解不等式组： $\text{[math]}$

答案解析收藏纠错 + 选题
19. (2021·门头沟模拟) 已知，如图， $\text{[math]}$ 是等边三角形， $\text{[math]}$ 于D ， E是BC延长线上的一点， $\text{[math]}$ ．求 $\text{[math]}$ 的度数．

答案解析收藏纠错 + 选题
20. (2021·门头沟模拟) 已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
21. (2021·门头沟模拟) 已知： $\text{[math]}$ ，CD平分 $\text{[math]}$ ．
求作：菱形DFCE ，使点F在BC边上，点E在AC边上，下面是尺规作图过程．

作法：①分别以C、D为圆心，大于 $\text{[math]}$ 为半径作弧，两弧分别交于点M、N；

②作直线MN分别与AC、BC交于点E、F；

③连接DE、DF ， DC与EF的交点记为点G；四边形DFCE为所求作的菱形．
1. （1）利用直尺和圆规依做法补全图形（保留作图痕迹）；
2. （2）完成下面的证明．
  证明： $\text{[math]}$ ，
  
  $\text{[math]}$ 为DC的垂直平分线．
  
  $\text{[math]}$ ，
  
  $\text{[math]}$ ．
  
  $\text{[math]}$ 平分 $\text{[math]}$ ，
  
  $\text{[math]}$ ．
  
  $\text{[math]}$ ，
  
  $\text{[math]}$ ▲ $\text{[math]}$ ▲ （）（填推理依据）
  
  同理可证 $\text{[math]}$ ，
  
  $\text{[math]}$ 四边形DFCE为平行四边形．
  
  又 $\text{[math]}$ ▲ ，
  
  $\text{[math]}$ 四边形DFCE为菱形．
答案解析收藏纠错 + 选题
22. (2021·门头沟模拟) 已知：如图，在菱形ABCD中， $\text{[math]}$ 于点E ，延长AD至F ，使 $\text{[math]}$ ，连接CF ．
1. （1）求证：四边形EBCF是矩形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求AF的长．
答案解析收藏纠错 + 选题
23. (2021·门头沟模拟) 在平面直角坐标系 $\text{[math]}$ 中，正比例函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象相交于点 $\text{[math]}$
1. （1）求k的值；
2. （2）过点 $\text{[math]}$ 平行于x轴的直线，分别与第一象限内的正比例函数 $\text{[math]}$ 、反比例函数 $\text{[math]}$ 的图象相交于 $\text{[math]}$ ，当 $\text{[math]}$ 时，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
24. (2021·门头沟模拟) 如图，AB是 $\text{[math]}$ 的直径，C是 $\text{[math]}$ 上一点，D是OB中点，过点D作AB的垂线交AC的延长线于点F ， FD上有一点E ， $\text{[math]}$ ．
1. （1）求证：CE是 $\text{[math]}$ 的切线；
2. （2）如果 $\text{[math]}$ ， $\text{[math]}$ ，求AB的长．
答案解析收藏纠错 + 选题
25. (2021·门头沟模拟) 2021年是中国共产党成立100周年，某中学面向学校全体师生征集“礼赞百年”活动作品，作品类别包括征文、书法、绘画．该中学学生小明统计了学校30个教学班上交活动作品的数量（单位：份），相关信息如下：
a ．小明所在中学30个教学班上交作品的数量统计图：

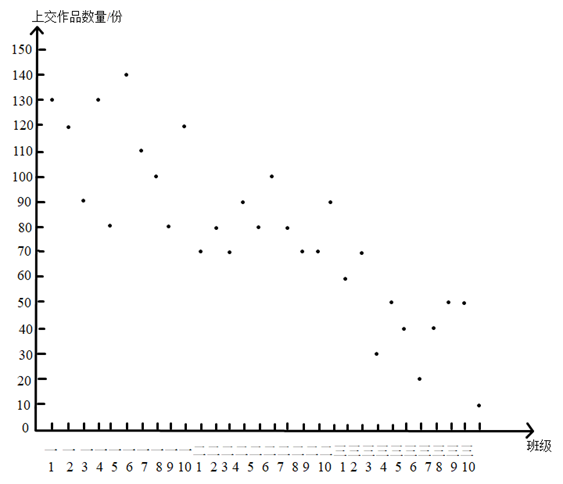b ．小明所在中学各班学生上交作品数量的平均数如下：

班级

初一年级（10个班）

初二年级（10个班）

初三年级（10个班）

平均数

110

80

40
1. （1）该中学各班学生上交作品数量的平均数约为（结果取整数）；
2. （2）已知该中学全体教师上交作品的数量恰好是该校各班级中，上交作品数量最多的班级与最少的班级的数量差，则全体教师上交作品的数量为份；
3. （3）记该中学初一年级学生上交作品数量的方差为 $\text{[math]}$ ，初二年级学生上交作品数量的方差为 $\text{[math]}$ ，初三年级学生上交作品数量的方差为 $\text{[math]}$ ．直接写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的大小关系．
答案解析收藏纠错 + 选题
26. (2021·门头沟模拟) 在平面直角坐标系 $\text{[math]}$ 中，已知关于x的二次函数 $\text{[math]}$
1. （1）求该二次函数的对称轴；
2. （2）若点 $\text{[math]}$ 在抛物线 $\text{[math]}$ 上，试比较m、n的大小；
3. （3） $\text{[math]}$ 是抛物线 $\text{[math]}$ 上的任意两点，若对于 $\text{[math]}$ 且 $\text{[math]}$ ，都有 $\text{[math]}$ ，求t的取值范围．
答案解析收藏纠错 + 选题
27. (2022八下·惠山期末) 在正方形ABCD中，将边AD绕点A逆时针旋转 $\text{[math]}$ 得到线段AE ， AE与CD延长线相交于点F ，过B作 $\text{[math]}$ 交CF于点G ，连接BE．
1. （1）如图1，求证： $\text{[math]}$ ；
2. （2）当（ $\text{[math]}$ ）时，依题意补全图2，用等式表示线段 $\text{[math]}$ 之间的数量关系，并证明．
答案解析收藏纠错 + 选题
28. (2021·门头沟模拟) 在平面直角坐标系 $\text{[math]}$ 中， $\text{[math]}$ 的半径为1，点A是平面内一点，过点A的直线交 $\text{[math]}$ 于点 B和点C（ $\text{[math]}$ ）， $\text{[math]}$ ，我们把点 B称为点A关于 $\text{[math]}$ 的“斜射点”．
1. （1）如图，在点 $\text{[math]}$ 中，存在关于 $\text{[math]}$ 的“斜射点”的是．
2. （2）已知若 $\text{[math]}$ ，点关于 $\text{[math]}$ 的“斜射点”为点B ，则点 B的坐标可以是．（写出两个即可）
3. （3）若点A直线 $\text{[math]}$ 上，点A关于 $\text{[math]}$ 的“斜射点”为 $\text{[math]}$ ，画出示意图，直接写出 k的取值范围．
答案解析收藏纠错 + 选题