

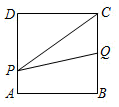
 B .
B .  C .
C .  D .
D . 


①以上化简步骤中,第一步进行的运算是()
A.整式乘法 B.因式分解
②第步开始出现错误,这一步错误的原因是;
甲班 | 82 | 85 | 96 | 73 | 91 | 99 | 87 | 91 | 86 | 91 |
87 | 94 | 89 | 96 | 96 | 91 | 100 | 93 | 94 | 99 |
乙班20名学生的成绩在D组中的数据是:93,91,92,94,92,92,92,甲乙两班抽取的学生成绩数据统计表如下:
班级 | 甲班 | 乙班 |
平均数 | 91 | 92 |
中位数 | 91 | b |
众数 | c | 92 |
方差 | 41.2 | 27.3 |

根据以上信息,解答下列问题:
课题 | 测量南山门最高点的高度 | |||
实物图 |
| |||
成员 | 组长:××× 组员:×××,×××,××× | |||
测量工具 | 卷尺,测角仪… | |||
测量示意图 |
| 说明:AB表示南山门最高点到地面的竖直距离,测角仪的高度CD=EF=1.5m,点C、F与点B在同一直线上,点C、F之间的距离可直接测得,且点A、B、C、D、E、F在同一平面内. | ||
测量数据 | 测量项目 | 第一次 | 第二次 | 平均值 |
α的度数 | 35.95° | 36.05° | 36° | |
β的度数 | 45.09° | 44.91° | 45° | |
C、F之间的距离 | 79.58m | 79.62m | 79.6m | |
… | … | |||
A书店:每套“名著经典”标价120元,若购买超过20套,超过部分按每套标价的八折出售;
B书店:每套“名著经典”标价120元,若购买超过15套,超过部分按每套标价的九折出售,然后每套再优惠10元.若用字母x表示购买“名著经典”的数量,字母y表示购买的价格,其函数图象如图所示.


已知:如图①,直线l与⊙O相交于点A、B,过点B作 .
求证:∠ABD= .

|
x/cm |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
y/cm |
9.49 |
7.62 |
5.83 |
|
3.16 |
3.16 |
4.24 |
请你通过计算补全表格;

如图1,△ABC与△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°,直线BD,CE交于点F,直线BD,AC交于点G.则线段BD和CE的数量关系是,位置关系是;
如图2,在△ABC和△ADE中,∠ABC=∠ADE=α,∠ACB=∠AED=β,直线BD,CE交于点F,AC与BD相交于点G.若AB=kAC,试判断线段BD和CE的数量关系以及直线BD和CE相交所成的较小角的度数,并说明理由;
如图3,在平面直角坐标系中,点M的坐标为(3.0),点N为y轴上一动点,连接MN.将线段MN绕点M逆时针旋转90得到线段MP,连接NP,OP.请直接写出线段OP长度的最小值及此时点N的坐标.