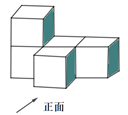
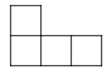
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 




七年级抽取的学生在C组的课外劳动时间为: .
八年级抽取的20名学生的课外劳动时间为: .
下表为七、八年级抽取的学生的课外劳动时间的统计量
| 年级 | 平均数 | 众数 | 中位数 | 方差 |
| 七年级 | 50 | 35 | a | 580 |
| 八年级 | 50 | b | 50 | 560 |

根据以上信息,解答下列问题:

|
如图,在正方形 |


