
 B .
B .  C .
C .  D .
D . 
①当地当年月平均气温的极差为 ;
②当地当年月平均气温的中位数为 ;
③当地当年月平均气温的平均数在 之间;
④小明家这5个月的月用水量随着月平均气温的变化而变化,温度越高,月用水量越大.
所有合理推断的序号是.
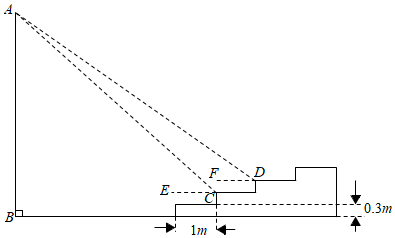

①当 时,求
的半径;
②当点 在
边上运动时,
半径的最小值为 ▲ .
(i)小红的思考
如图,先任意画出一个 ,然后按下列作法,作出一个满足条件的
,作法如下:

①作 的外接圆
②过点 作
,与
交于点
③连接 (点
与
重合),
(点
与
重合),得到
请说明小红所作的 .
(ii)小明的思考
如图,对于满足条件的 ,
和高
,
;小明将
通过图形的变换,使边
与
重合,
,
相交于点
,连接
,易证

接下来,小明的证明途径可以用下面的框图表示,请填写其中的空格.

如图,在 和
中,
,
分别是
和
的高,(
),且
,
,求证:
.
