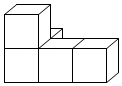
 B .
B . 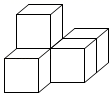 C .
C . 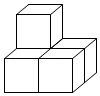 D .
D . 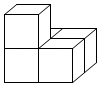
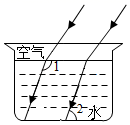
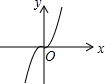 B .
B . 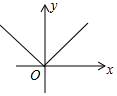 C .
C . 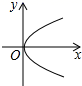 D .
D . 



| 已知钝角 步骤一:以点 步骤二:以点 步骤三:连接 |
下面是四位同学对其做出的判断:
小明说: ;
小华说: ;
小强说: ;
小方说: .
则下列说法正确的是( )
如图,直线y= 与y轴交于点A,与直线y=﹣
交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣
上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )


根据统计图提供的信息,解答下列问题:
| | | |
| 进价 | 120元/件 | 100元/件 |
| 售价 | 138元/件 | 120元/件 |



①如图2,当∠ACB=90°,连接PQ,求PQ;
②如图3,当∠ACB≠90°,点M、N分别是AC、AP中点连接MN.若MN= ,则S△ABC= ▲ .