陕西省汉中市汉台区2021年数学中考一模试卷

更新时间：2021-06-29 浏览次数：245 类型：中考模拟

一、单选题

1. (2024九下·贵阳模拟) $\text{[math]}$ 的倒数是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·东平模拟) 下图是某个几何体的三视图，该几何体是（）

A . 长方体 B . 正方体 C . 圆柱 D . 三棱柱

答案解析收藏纠错 + 选题
3. (2021·汉台模拟) 如图，直线 $\text{[math]}$ 被 $\text{[math]}$ 所截， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021·汉台模拟) 已知 $\text{[math]}$ ，则正比例函数 $\text{[math]}$ 的图象经过（　　）

A . 第二、四象限， B . 第二、三象限 C . 第一、三象限 D . 第一、四象限

答案解析收藏纠错 + 选题
5. (2021·汉台模拟) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021八下·雄县期末) 如图， $\text{[math]}$ ABC中，AB＝AC＝12，BC＝10，AD平分∠BAC交BC于点D，点E为AC的中点，连接DE，则 $\text{[math]}$ CDE的周长为（）

A . 11 B . 17 C . 18 D . 16

答案解析收藏纠错 + 选题
7. (2021八上·淮北月考) 若直线 $\text{[math]}$ 沿y轴平移3个单位得到新的直线 $\text{[math]}$ ，则b的值为（）

A . -2或4 B . 2或-4 C . 4或-6 D . -4或6

答案解析收藏纠错 + 选题
8. (2021八下·武义期中) 如图，矩形 $\text{[math]}$ 中，点 $\text{[math]}$ 在 $\text{[math]}$ 上，且 $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则矩形 $\text{[math]}$ 的面积为（）

A . $\text{[math]}$ B . 24 C . $\text{[math]}$ D . 12

答案解析收藏纠错 + 选题
9. (2021·汉台模拟) 如图，△ABC内接于⊙O，BD是⊙O的直径.若∠DBC＝33°，则∠A等于（）

A . 33° B . 57° C . 67° D . 66°

答案解析收藏纠错 + 选题
10. (2021八上·平阳期中) 对于二次函数y＝x²﹣4x＋3，当自变量x满足a≤x＜3时，函数值y的取值范围为﹣1≤y＜0，则a的取值范围为（）

A . ﹣1＜a≤2 B . 1＜a≤3 C . 1＜a＜2 D . 1＜a≤2

答案解析收藏纠错 + 选题

二、填空题

11. (2020八上·孝南月考) 一个正多边形的每一个外角都等于36 $\text{[math]}$ ，则这个多边形的边数是．

答案解析收藏纠错 + 选题
12. (2021·汉台模拟) 如图，正比例函数y＝x和反比例函数y＝ $\text{[math]}$ （k≠0）的图象在第一象限交于点A，且OA＝2，则k的值为.

答案解析收藏纠错 + 选题
13. (2021·汉台模拟) 如图，平行四边形ABCD中，∠DAB=60°，AB=6，BC=2，P为边CD上的一动点，则 $\text{[math]}$ 的最小值等于.

答案解析收藏纠错 + 选题

三、解答题

14. (2021·汉台模拟) 解不等式组： $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2021·汉台模拟) 化简： $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2021·汉台模拟) 如图，△ABC中，AB＝AC，∠A＝36°.请利用尺规作图法在AC上求作一D，使得BD把△ABC分成两个等腰三角形.（保留作图痕迹，不写作法）

答案解析收藏纠错 + 选题
17. (2020八上·莘县期末) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
求证： $\text{[math]}$ .

答案解析收藏纠错 + 选题

18. (2023·青岛模拟) 某学校开展了主题为“垃圾分类，绿色生活新时尚”的宣传活动.为了解学生对垃圾分类知识的掌握情况，学校从全校学生中随机抽取部分学生进行知识测试（测试满分100分，得分均为整数），并对成绩进行整理、描述和分析.部分信息如下：

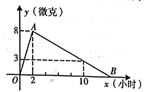
a.成绩频数分布表与扇形统计图：

学生测试成绩的频数表

组别	成绩a（分）	频数（人）	各组总分数（分）
A	50≤a＜60	10	552
B	60≤a＜70	15	971
C	70≤a＜80	m	1512
D	80≤a＜90	40	3393
E	90≤a≤100	15	1422

b.成绩在60≤a＜70这一组的是：60 62 64 65 66 66 67 67 67 68 69 65 61 63 67

根据以上信息，回答下列问题：

（1）填空：m＝，n＝，所抽取学生成绩在60≤a＜70这一组的众数是分；
（2）求所抽取学生的平均成绩；
（3）若该校有1400名学生，假设全部参加此次测试，请估计成绩不低于80分的人数.

答案解析收藏纠错 + 选题

19. (2021·汉台模拟) 如图，某地有一座古楼，小华和数学组的成员想用所学知识测量古楼的高AB.测量方法如下：首先，小华站在D处，用测角仪测得古楼顶端A的仰角为50.3°；然后，小华在点N处竖立高2米的标杆MN，接着沿DN后退到点F，恰好看到标杆顶端M和古楼顶端A在一条直线上.量得小华的眼睛到地面的距离CD＝EF＝1.5米，NF＝1米，DF＝68米.测量示意图如图所示，已知点D、B、N、F在一条直线上，CD⊥DF，AB⊥DF，MN⊥DF，EF⊥DF，求这座古楼的高AB.（参考数据：sin50.3°≈0.77，cos50.3°≈0.64，tan50.3°≈1.20）

答案解析收藏纠错 + 选题
20. (2021·汉台模拟) 在全球关注的抗击“新冠肺炎”中某跨国科研中心的一个团队研制了一种助治“新冠附炎”的新药，在试验药效时发现，如果成人按规定的制量服用，那么服药后2小时血液中含药量最高，达每毫升8微克（1微克= $\text{[math]}$ 毫克），接着逐步安减，10小时时血液中含药最为每毫升3微克，每毫升血液中含药量 $\text{[math]}$ （微克）随时间 $\text{[math]}$ （小时）的变化如图所示.
1. （1）分别求线段 $\text{[math]}$ 所表示的函数关系式；
2. （2）如果每毫升血液中含药量为4微克或4微克以上时对治病是有效的，那么这个有效时间是多长？
答案解析收藏纠错 + 选题
21. (2021·汉台模拟) 2022年北京冬奥会吉祥物“冰墩墩”以熊猫为原型进行设计创作，北京冬残奥会吉祥物“雪容融”则以中国标志性符号的灯笼为创意进行设计创作“冰墩墩”和“雪容融”是一个非常完美的搭：配和组合，是中国文化和奥林匹克精神又一次完美的结合莉莉有“冰墩墩”和“雪容融”的纪念邮票各2张（如图），这4张邮票背面完全相同，莉莉想给好友小婷和小华各送一张纪念邮票，她先让小婷从这4张邮票中随机抽取一张，然后，再让小华从剩下的3张中随机抽取一张.
1. （1）小婷抽到“冰墩墩”的纪念邮票的概率是.
2. （2）利用树状图或列表法求小婷和小华均抽到“雪容融”的纪念邮票的概率.
答案解析收藏纠错 + 选题
22. (2023·西安模拟) 如图，AB为⊙O的直径，弦CD⊥AB，垂足为点P，直线BF与AD延长线交于点F，且∠AFB＝∠ABC.
1. （1）求证：直线BF是⊙O的切线；
2. （2）若tan∠BCD＝ $\text{[math]}$ ，OP＝1，求线段BF的长.
答案解析收藏纠错 + 选题
23. (2021·汉台模拟) 如图，抛物线L：y＝﹣x²＋bx＋c与x轴交于点A（﹣1，0），且抛物线过点B（﹣4，﹣3），顶点为C.
1. （1）求抛物线L的函数表达式及顶点C的坐标；
2. （2）抛物线L′与抛物线L关于原点O对称，抛物线L′与x轴交于点M、N（点M在点N的左侧），在点N右侧的抛物线L′上是否存在一点P，作PD⊥x轴于点D，使得以点P，M，D为顶点的三角形与△ABC相似？若存在，求出P点坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
24. (2021·汉台模拟) 如图

问题探究
1. （1）如图①，在△ABC中，∠C＝90°，BD平分∠ABC，AB＝6，CD＝2，则△ABD的面积为；
2. （2）如图②，在△ABC中，∠BAC＝30°，BC边上的高AD＝7，△ABC外接圆的半径为4，求△ABC的面积；
3. （3）如图③，现要修建一个形状为△ABC的水上乐园，并在BC边上的点D处建一个储物间，其中∠BAC＝60°，AD平分∠BAC且AD＝300m，为节约成本，水上乐园管理部门计划使△ABC的面积尽可能的小，问能否修建一个满足要求的面积最小的△ABC？若能，请求出△ABC的最小面积，若不能，请说明理由.（结果保留根号）
答案解析收藏纠错 + 选题