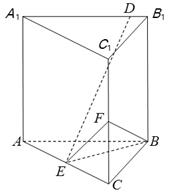
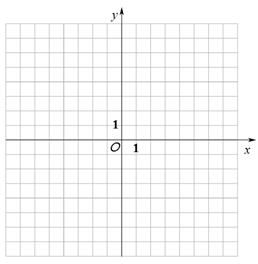
B .
B .  C .
C .  D .
D . 
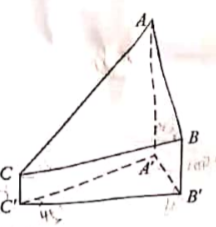
|
一级品 |
二级品 |
合计 |
|
|
甲机床 |
150 |
50 |
200 |
|
乙机床 |
120 |
80 |
200 |
|
合计 |
270 |
130 |
400 |
附:
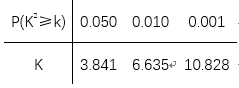
①数列{an}是等差数列:②数列{ }是等差数列;③a2=3a1
注:若选择不同的组合分别解答,则按第一个解答计分.