山西省临汾市洪洞县2021年中考数学二模试卷

更新时间：2024-07-13 浏览次数：253 类型：中考模拟

一、单选题

1. (2021·洪洞模拟) 下列数中比﹣2小的数是（　　）

A . ﹣ $\text{[math]}$ B . ﹣3 C . 0 D . 2

答案解析收藏纠错 + 选题
2. (2023九下·阳朔模拟) 现实生活中，对称现象无处不在，中国的方块字中也有些具有对称性，下列美术字既是轴对称图形又是中心对称图形的是（　　）

A . 吕 B . 人 C . 甲 D . 日

答案解析收藏纠错 + 选题
3. (2024九下·松山月考) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021·洪洞模拟) 在人类生活中，早就存在着收入与支出，盈利与亏本等具有相反意义的现象，可以用正负数表示这些相反意义的量．我国古代数学名著《九章算术》一书中也明确提出“正负术”．最早使用负数的国家是（　　）

A . 印度 B . 法国 C . 阿拉伯 D . 中国

答案解析收藏纠错 + 选题
5. (2021·洪洞模拟) 某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原正方体中，与“绣”字所在面相对的面上的汉字是（　　）

A . 惟 B . 愿 C . 山 D . 河

答案解析收藏纠错 + 选题
6. (2021七下·侯马期中) 不等式组 $\text{[math]}$ 的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2021·洪洞模拟) 为大力发展现代农业，山西省连续多年整合各项相关资金设立了农田建设补助专项资金，用于支持高标准农田建设.2020年省级财政在许多支出大幅压减的情况下，仍下达农田建设补助资金约14.5亿元，与2019年相比增长率约为16%，则2020年比2019年农田建设补助资金增加了（　　）

A . 2亿元 B . 2.5亿元 C . 3亿元 D . 3.5亿元

答案解析收藏纠错 + 选题
8. (2021·洪洞模拟) 在中考体育训练期间，小宇对自己某次实心球训练的录像进行分析，发现实心球飞行高度y（米）与水平距离x（米）之间的关系式为 $\text{[math]}$ ，由此可知小宇此次实心球训练的成绩为（　　）

A . $\text{[math]}$ 米 B . 8米 C . 10米 D . 2米

答案解析收藏纠错 + 选题

9. (2021·洪洞模拟) 函数y₁ ， y₂与自变量x的部分对应值如表所示：

x	﹣6	﹣4	﹣2	0	2	4	6
y₁	﹣ $\text{[math]}$	﹣2	﹣4		4	2	$\text{[math]}$
y₂	﹣4	﹣2	0	2	4	6	8

下列结论：①y₁是x的反比例函数；②y₂是x的一次函数；③当x＜0时，y₁ ， y₂都随x的增大而增大；④y₁＞y₂时，x＜﹣4．其中所有正确结论的序号是（　　）

A . ①②④ B . ②③④ C . ①②③ D . ①②

答案解析收藏纠错 + 选题

10. (2021·安丘模拟) 如图，在半径为2的⊙O中，将劣弧AB沿弦AB翻折，折叠后的弧AB恰好与OA、OB相切，则阴影部分的面积为（　　）．

A . 4﹣π B . 4+π C . π﹣2 D . π+2

答案解析收藏纠错 + 选题

二、填空题

11. (2024八上·江阴期中) 2的平方根是．

答案解析收藏纠错 + 选题
12. (2021·洪洞模拟) 据国家医保局统计，2020年累计结算新冠肺炎患者医疗费用28.4亿元，28.4亿元用科学记数法表示为元．

答案解析收藏纠错 + 选题
13. (2021七下·新泰期中) 小明家的客厅地板如图所示，一个小球在地板上任意滚动，并随机停留在某块地板砖上，每块地板砖的大小质地完全相同，那么小球停留在黑色区域的概率是．

答案解析收藏纠错 + 选题
14. (2021·洪洞模拟) 如图是一组有规律的图案，它们是由大小相同的☆摆放而成，第1个图案有3个☆，第2个图案有7个☆，第3个图案有13个☆，第4个图案有21个☆，…按此规律摆下去，第n个图案有个☆（用含n的代数式表示）．

答案解析收藏纠错 + 选题
15. (2021·洪洞模拟) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为边 $\text{[math]}$ 上两点，将矩形 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，点 $\text{[math]}$ 恰好落在 $\text{[math]}$ 上的 $\text{[math]}$ 处，且 $\text{[math]}$ ，再将矩形 $\text{[math]}$ 沿过点 $\text{[math]}$ 的直线折叠，使点 $\text{[math]}$ 落在 $\text{[math]}$ 上的 $\text{[math]}$ 处，折痕交 $\text{[math]}$ 于点 $\text{[math]}$ ，将矩形 $\text{[math]}$ 再沿 $\text{[math]}$ 折叠， $\text{[math]}$ 与 $\text{[math]}$ 恰好重合，已知 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题

16. (2021·洪洞模拟)
1. （1）计算： $\text{[math]}$ ﹣（π﹣1）⁰﹣6tan30°+（﹣ $\text{[math]}$ ）^﹣2 ．
2. （2）化简： $\text{[math]}$ ÷ $\text{[math]}$ ﹣ $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. (2021·洪洞模拟) 如图，△ABC是⊙O的内接三角形，BD为⊙O的直径，过点C作CE⊥BD ，垂足为E ．
1. （1）求证：∠BAC＝∠BCE；
2. （2）若∠BAC＝60°，CE＝3，求BD的长．
答案解析收藏纠错 + 选题
18. (2021·洪洞模拟) 行业景气指数是综合反映某一特定调查群体或某一社会经济现象所处的状态或发展趋势的一种指标（景气指数＞100，处于景气状态；景气指数＜100，处于不景气状态）.2020年第四季度对千余家战略性新兴产业典型企业的调查结果显示，在一系列稳增长政策作用下，第四季度战略性新兴产业已经基本摆脱疫情带来的不良影响，各项指标全线上升．如图1是2020年第四季度部分新兴产业的行业景气指数及环比增速统计图（环比增速＝ $\text{[math]}$ ×100%）．
1. （1）请根据统计图解答下列问题：
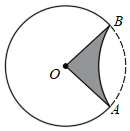
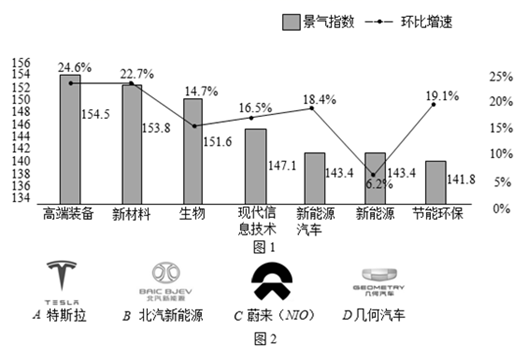
  ①图中统计的七个行业中，环比增速的中位数是 ▲ ．
  
  ②请你根据上面统计图中的数据，对统计的七个行业进行简单评价．（写出一条即可）
2. （2）小明对上述七个行业中的新能源汽车行业最感兴趣，他上网查阅了相关资料，找到四个新能源汽车的图标（如图2），并将其制成A ， B ， C ， D四张卡片（除编号和内容外，其余完全相同）．他将这四张卡片背面朝上，洗匀放好，从中随机抽取一张（不放回），再从中随机抽取一张．请用列表或画树状图的方法求抽到两张卡片恰好是“几何汽车”和“蔚来（NIO）”的概率．
答案解析收藏纠错 + 选题
19. (2021·洪洞模拟) 平遥牛肉久负盛名．据史料记载，清代时已誉满三晋．其制作工艺独特，用料讲究，所产牛肉营养丰富，具有扶胃健脾之功效．某特产店以每千克110元的价格购进一批平遥牛肉，当按每千克140元的价格出售时，平均每天可销售30千克．“十一”期间，为了尽可能扩大销售量，商家决定降价销售．经调查发现，每千克降价1元，每天可多卖2千克．若该经销商想要每天获利1000元，则每千克应降价多少元？

答案解析收藏纠错 + 选题
20. (2021·洪洞模拟) 阅读与思考：

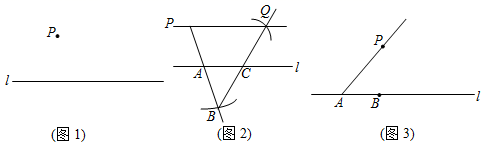
如图是小宇同学的数学日记，请仔细阅读，并完成相应的任务．

x年x月x日星期日．

过直线外一点作这条直线的平行线．

已知：如图1，点P为直线l外一点，

求作：直线PQ ，使得PQ∥l ．

今天，我们组的小明和小红的作法和我不同．

小明：如图2，①在直线l上取一点A ，作射线PA ，以点A为圆心，AP长为半径画弧，交射线PA于点B；

②直线l上取一点C（不与点A重合），作射线BC ，以点C为圆心，CB长为半径画弧，交射线BC于点Q；

③作直线PQ ，则直线PQ就是所求作的直线．

小红：如图3，①在直线l上取A ， B两点，作射线AP；

②作∠PAB的角平分线AC；

③以点P为圆心，PA长为半径画弧，交射线AC于点Q；

④作直线PQ ．则直线PQ就是所求作的直线．

我有如下思考：以上两种办法依据的是什么数学原理呢？

任务：
1. （1）填空：小明的作法依据的一个数学定理是；
2. （2） ①使用直尺和圆规，根据小红的作法补全图3；（保留作图痕迹）
  ②根据小红的操作过程，证明PQ∥l ．
答案解析收藏纠错 + 选题
21. (2021·洪洞模拟) 随着精准扶贫政策的落地实施，小亮家所在的村落进行了整村搬迁，小亮同家人一起告别了祖辈们世代居住的窑洞，搬进了宽敞明亮的新房．他家的新房全部安装的是内倒式窗户．为帮助家人确定窗边家具摆放位置，小亮想要知道开启窗扇时，窗扇顶端向屋内移动的水平距离．如图，小亮测得窗扇高度AB＝80cm ，开启时的最大张角∠A＝22.5°，窗扇开启后的位置为AB'．
1. （1）请根据这些数据帮助小亮计算开启窗扇时，窗扇顶端向屋内移动的最大水平距离（不考虑窗扇的厚度，参考数据sin22.5°≈0.38，cos22.5°≈0.92，tan22.5°≈0.41）；
2. （2）小亮的爸爸说：“咱家安装窗户总共花了4800元，隔壁小明家安装的是平移式窗户，他家窗户总面积比咱家多3平方米，但他家总共才花了3680元，咱家安装的这种内倒式窗户每平方米的价格是小明家安装的平移式窗户每平方米价格的1.5倍.”请你根据以上信息求出小亮家安装的这种内倒式窗户每平方米多少元？
答案解析收藏纠错 + 选题
22. (2021·洪洞模拟) 综合与实践．
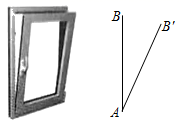
问题情境：

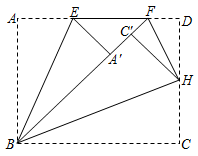
综合与实践课上，同学们开展了以“图形的旋转”为主题的数学活动．

实践操作：

如图1，将等腰Rt△AEF绕正方形ABCD的顶点A逆时针方向旋转，其中∠AEF＝90，EA＝EF ，连接CF ，点H为CF的中点，连接HD ， HE ， DE ，得到△DHE ．

应用探究：
1. （1）勤奋组：
  如图2，当点E恰好落在正方形ABCD的对角线AC上时，判断△DHE的形状，并说明理由；
2. （2）善思组：
  如图3，当点E恰好落在正方形ABCD的边AB上时，（1）中的结论还成立吗？请说明理由；
3. （3）创新小组：
  发现若连接BE ，在旋转Rt△AEF的过程中， $\text{[math]}$ 为定值，请你直接写出其值．
答案解析收藏纠错 + 选题
23. (2021·洪洞模拟) 综合与探究
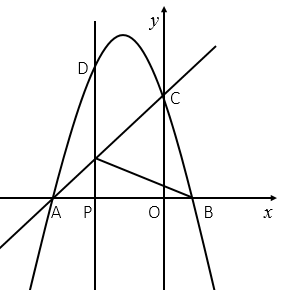
如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴分别交于点 $\text{[math]}$ 和点 $\text{[math]}$ （点 $\text{[math]}$ 在点 $\text{[math]}$ 的左侧），交 $\text{[math]}$ 轴于点 $\text{[math]}$ ．点 $\text{[math]}$ 是线段 $\text{[math]}$ 上的一个动点，沿 $\text{[math]}$ 以每秒1个单位长度的速度由点 $\text{[math]}$ 向点 $\text{[math]}$ 运动，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴，交抛物线于点 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求直线 $\text{[math]}$ 的表达式；
2. （2）在点 $\text{[math]}$ 运动过程中，运动时间 $\text{[math]}$ 为何值时， $\text{[math]}$ ？
3. （3）在点 $\text{[math]}$ 运动过程中， $\text{[math]}$ 的周长是否存在最小值？若存在，求出此时点 $\text{[math]}$ 的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题