题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /中考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

四川省眉山市青神县2021年数学中考一诊试卷

更新时间：2021-06-29 浏览次数：229 类型：中考模拟

一、单选题

1. (2024九下·息县模拟) $\text{[math]}$ 的倒数是（）

A . -2 B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·仁寿模拟) 下列等式成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九下·中江模拟) 据生物学可知，卵细胞是人体细胞中最大的细胞，其直径约为0.0002米．将数0.0002用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·江门模拟) 如图，下列几何体的左视图不是矩形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2021·青神模拟) 下列事件：①对顶角相等，②矩形的对角线相等，③同位角相等，④平行四边形是中心对称图形，其中不是必然事件的是（）

A . ① B . ②③ C . ③ D . ④

答案解析收藏纠错 + 选题
6. (2022九上·聊城期末) 如图，正五边形 $\text{[math]}$ 内接于 $\text{[math]}$ ，点 $\text{[math]}$ 是劣弧 $\text{[math]}$ 上一点（点 $\text{[math]}$ 不与点 $\text{[math]}$ 重合），则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021·青神模拟) 如图，Rt△ABC中，∠C＝90°，用尺规分别截取BE ， BD ，使BE＝BD ，分别以D、E为圆心、以大于 $\text{[math]}$ 的长为半径作弧，两弧在∠CBA内交于点F；作射线BF交AC于点G ．若CG＝1，P为AB上一动点，则GP的最小值为（）

A . 无法确定 B . $\text{[math]}$ C . 1 D . 2

答案解析收藏纠错 + 选题
8. (2023八上·云阳县期中) 如果等腰三角形的一个角是80°，那么它的底角是（）

A . 80°或50° B . 50°或20° C . 80°或20° D . 50°

答案解析收藏纠错 + 选题
9. (2021九上·金东期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . ﹣1 B . 1 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023八上·赵县月考) 在螳螂的示意图中，AB∥DE，△ABC是等腰三角形，∠ABC＝124°，∠CDE＝72°，则∠ACD＝（）

A . 16° B . 28° C . 44° D . 45°

答案解析收藏纠错 + 选题
11. (2021·青神模拟) 如图，矩形ABCD对角线AC、BD相交于点O，点P是AD边上的一个动点，过点P分别作PE⊥AC于点E，PF⊥BD于点F，若AB＝3，BC＝4，则PE＋PF的值为（）

A . 10 B . 9.6 C . 4.8 D . 2.4

答案解析收藏纠错 + 选题
12. (2021·青神模拟) 如图，在△ABC中，AB=AC，AD和CE是高，∠ACE=45°，点F是AC的中点，AD与FE，CE分别交于点G、H，∠BCE=∠CAD，有下列结论：①图中存在两个等腰直角三角形；②△AHE≌△CBE；③BC•AD= $\text{[math]}$ AE²；④S_△_ABC=4S_△_ADF ．其中正确的个数有（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题

13. (2022七下·慈利期中) 因式分解： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2021·青神模拟) 已知 $\text{[math]}$ 、 $\text{[math]}$ 是方程 $\text{[math]}$ 的两个实数根，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2021·青神模拟) 若一次函数 $\text{[math]}$ 中， $\text{[math]}$ 随 $\text{[math]}$ 的增大而增大，且它的图象与 $\text{[math]}$ 轴交于正半轴，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2021·青神模拟) 若关于x的方程 $\text{[math]}$ 有增根，则a的值是.

答案解析收藏纠错 + 选题
17. (2023·济南模拟) 如图，在边长为2的正方形ABCD中，对角线AC的中点为O，分别以点A，C为圆心，以AO的长为半径画弧，分别与正方形的边相交，则图中的阴影部分的面积为.（结果保留π）

答案解析收藏纠错 + 选题
18. (2021·青神模拟) 如图，菱形OABC在第一象限内，∠AOC＝60°，反比例函数 $\text{[math]}$ （x＞0）的图象经过点A，交BC边于点D，若△AOD的面积为 $\text{[math]}$ ，则k的值为.

答案解析收藏纠错 + 选题

三、解答题

19. (2022·峨边模拟) 计算： $\text{[math]}$ ﹣2sin30°﹣|1﹣ $\text{[math]}$ |+（ $\text{[math]}$ ）^﹣²﹣（π﹣2020）⁰ ．

答案解析收藏纠错 + 选题
20. (2021·青神模拟) 解不等式组 $\text{[math]}$ ，把其解集在数轴上表示出来，并写出它的整数解.

答案解析收藏纠错 + 选题
21. (2021·青神模拟) 如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，△ABC的三个顶点坐标分别为A（-3，1），B（-1，1），C（0，3）.

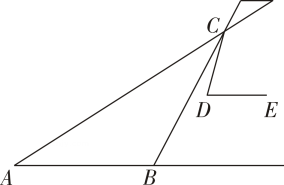
（ 1 ）画出△ABC关于y轴对称的△ $\text{[math]}$ ；

（ 2 ）画出△ABC以点O为位似中心的位似图形△ $\text{[math]}$ ，△ABC与△ $\text{[math]}$ 的位似比为1：2；

（ 3 ）求以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 四个点为顶点构成的四边形的面积.

答案解析收藏纠错 + 选题
22. (2021·怀化模拟) 2020年5月5日，为我国载人空间站工程研制的长征五号运较火箭在海南文昌首飞成功．运载火箭从地面 $\text{[math]}$ 处发射、当火箭到达点 $\text{[math]}$ 时，地面 $\text{[math]}$ 处的雷达站测得 $\text{[math]}$ 米，仰角为 $\text{[math]}$ .3秒后，火箭直线上升到达点 $\text{[math]}$ 处，此时地面 $\text{[math]}$ 处的雷达站测得 $\text{[math]}$ 处的仰角为 $\text{[math]}$ ．已知 $\text{[math]}$ 两处相距 $\text{[math]}$ 米，求火箭从 $\text{[math]}$ 到 $\text{[math]}$ 处的平均速度（结果精确到 $\text{[math]}$ 米，参考数据： $\text{[math]}$ ）

答案解析收藏纠错 + 选题

23. (2021·青神模拟) 某校八年级甲、乙两班各有学生50人，为了了解这两个班学生身体素质情况，进行了抽样调查，过程如下，请补充完整.

（1）收集数据：从甲、乙两个班各随机抽取10名学生进行身体素质测试，测试成绩（百分制）如下：

甲班65 75 75 80 60 50 75 90 85 65

乙班90 55 80 70 55 70 95 80 65 70

整理描述数据：按如下分数段整理、描述这两组样本数据：

成绩x

人数

班级

50≤x＜60

60≤x＜70

70≤x＜80

80≤x＜90

90≤x≤100

甲班

1

3

3

2

1

乙班

2

1

m

2

n

在表中：m=，n=.

（2）分析数据：
①两组样本数据的平均数、中位数、众数如表所示：

班级

平均数

中位数

众数

甲班

72

x

75

乙班

72

70

y

在表中：x= ▲ ，y= ▲ .

②若规定测试成绩在80分（含80分）以上的学生身体素质为优秀，请估计乙班50名学生中身体素质为优秀的学生有 ▲ 人.

③现从甲班指定的2名学生（1男1女），乙班指定的3名学生（2男1女）中分别抽取1名学生去参加上级部门组织的身体素质测试，用树状图和列表法求抽到的2名同学是1男1女的概率.

答案解析收藏纠错 + 选题

24. (2021·青神模拟) 某商场同时购进甲、乙两种商品共200件，其进价和售价如表，设其中甲种商品购进x件

商品名称

甲

乙

进价（元/件）

80

100

售价（元/件）

160

240
1. （1）若该商场购进这200件商品恰好用去17900元，求购进甲、乙两种商品各多少件？
2. （2）若设该商场售完这200件商品的总利润为y元.
  ①求y与x的函数关系式；
  
  ②该商品计划最多投入18000元用于购买这两种商品，则至少要购进多少件甲商品？若售完这些商品，则商场可获得的最大利润是多少元？
答案解析收藏纠错 + 选题
25. (2021·青神模拟) 综合与实践
问题情境：

如图①，点E为正方形ABCD内一点，∠AEB＝90°，将Rt△ABE绕点B按顺时针方向旋转90°，得到△CBE′（点A的对应点为点C）.延长AE交CE′于点F，连接DE.

猜想证明：
1. （1）试判断四边形BE'FE的形状，并说明理由；
2. （2）如图②，若DA＝DE，请猜想线段CF与FE'的数量关系并加以证明；
3. （3）如图①，若AB＝15，CF＝3，请直接写出DE的长.
答案解析收藏纠错 + 选题
26. (2021·青神模拟) 如图，抛物线 $\text{[math]}$ 与x轴交于A、B两点（点A在点B左边），与y轴交于点C.直线 $\text{[math]}$ 经过B、C两点.
1. （1）求抛物线的解析式；
2. （2）点P是抛物线上的一动点，过点P且垂直于x轴的直线与直线 $\text{[math]}$ 及x轴分别交于点D、M. $\text{[math]}$ ，垂足为N.设 $\text{[math]}$ .
  ①点P在抛物线上运动，若P、D、M三点中恰有一点是其它两点所连线段的中点（三点重合除外）.请直接写出符合条件的m的值；
  
  ②当点P在直线 $\text{[math]}$ 下方的抛物线上运动时，是否存在一点P，使 $\text{[math]}$ 与 $\text{[math]}$ 相似.若存在，求出点P的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题

试卷信息