题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /中考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

陕西省初中数学历年真题与模拟汇编：图形2

更新时间：2021-07-09 浏览次数：170 类型：二轮复习

一、单选题

1. (2021·陕西模拟) 如图， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021·陕西模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，若 $\text{[math]}$ 为劣弧 $\text{[math]}$ 上的一点， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021·陕西模拟) 如图，直线l₁ $\text{[math]}$ l₂ ， ∠1＝50°，∠2＝23°20′，则∠3的度数为（）

A . 26°40′ B . 27°20′ C . 27°40′ D . 73°20′

答案解析收藏纠错 + 选题
4. (2021·渭滨模拟) 如图，已知AB∥CD，∠1＝125°，∠2＝55°，则∠C＝（）

A . 45° B . 50° C . 70° D . 65°

答案解析收藏纠错 + 选题
5. (2021·兰州模拟) 如图，直线 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，那么 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023八下·临沂期中) 如图，将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起，其中点A′与点A重合，点C′落在边AB上，连接B′C．若∠ACB=∠AC′B′=90°，AC=BC=3，则B′C的长为（）

A . 3 $\text{[math]}$ B . 6 C . 3 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020九上·饶阳期末) 如图，在矩形ABCD中，AB=2，BC=3．若点E是边CD的中点，连接AE，过点B作BF⊥AE交AE于点F，则BF的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021·陕西模拟) 如图，点A，D，B，C是圆O上的四个点，连接AB，CD，相交于点E，若∠BOD＝40°，∠AOC＝120°，则∠AEC等于（）

A . 70° B . 75° C . 80° D . 85°

答案解析收藏纠错 + 选题
9. (2021八下·南宁期中) 如图，菱形 $\text{[math]}$ 对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ .若菱形 $\text{[math]}$ 的面积为4，则菱形的边长为（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
10. (2021·陕西模拟) 如图，点E是矩形ABCD的边CD上一点，作AF⊥BE于F，连接DF，若AB＝6，DF＝BC，则CE的长度为（）

A . 2 B . $\text{[math]}$ C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2021·陕西模拟) 如图，已知 $\text{[math]}$ 中，CD⊥AB，垂足为D，CE平分∠ACD交AD于E，若CD＝12，BC＝13，且 $\text{[math]}$ 的面积为48，则点E到AC的距离为（）

A . 5 B . 3 C . 4 D . 1

答案解析收藏纠错 + 选题
12. (2021·陕西模拟) 如图，AB是⊙O的直径，弦CD⊥AB，DE∥CB交⊙O于点E，若∠CBA＝20°，则∠AOE的度数为（）

A . 120° B . 80° C . 110° D . 100°

答案解析收藏纠错 + 选题
13. (2021·陕西模拟) 如图，在⊙O中，点A、B、C均在圆上，连接OA，OB，OC，BC，AC，若AC $\text{[math]}$ OB，OC＝4，AB＝5，则BC＝（）

A . 5 B . $\text{[math]}$ C . $\text{[math]}$ D . 8

答案解析收藏纠错 + 选题
14. (2021·渭滨模拟) 如图，AB是⊙O的直径，弦CD交AB于点E，且AE＝CD＝16，∠BAC＝ $\text{[math]}$ ∠BOD，则⊙O的半径为（）

A . 4 $\text{[math]}$ B . 8 C . 10 D . 6

答案解析收藏纠错 + 选题
15. (2021八下·海曙月考) 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 长（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
16. (2022·陈仓模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 的角平分线， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 长是（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
17. (2021·雁塔模拟) 如图，已知⊙O为四边形ABCD的外接圆，O为圆心，若∠BCD＝120°，AB＝AD＝6，则⊙O的半径长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题

二、填空题

18. (2021·陕西模拟) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .以 $\text{[math]}$ 为边作正方形 $\text{[math]}$ .点M是边 $\text{[math]}$ 上一动点，连接 $\text{[math]}$ ，过O作 $\text{[math]}$ 的垂线，垂足为N，连接 $\text{[math]}$ .则线段 $\text{[math]}$ 的最小值是.

答案解析收藏纠错 + 选题
19. (2021·陕西模拟) 如图，A、B、C、D为一个外角为40°的正多边形的顶点，若O为正多边形的中心，则∠OAD＝°.

答案解析收藏纠错 + 选题
20. (2020九上·安阳期中) 如图，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，连接AC．若AC=6，则四边形ABCD的面积为．

答案解析收藏纠错 + 选题

三、解答题

21. (2021·渭滨模拟) 如图，△ABC中，点D、E在边BC上，∠ADC＝∠AEB，CD＝BE.求证：∠BAD＝∠CAE.

答案解析收藏纠错 + 选题
22. (2016·陕西)
如图，在▱ABCD中，连接BD，在BD的延长线上取一点E，在DB的延长线上取一点F，使BF=DE，连接AF、CE．
求证：AF∥CE．

答案解析收藏纠错 + 选题
23. (2023·济南模拟) 如图，在▱ABCD中，点E，F是对角线AC上的两点，且AF=CE，连接DE，BF.求证：DE∥BF.

答案解析收藏纠错 + 选题
24. (2021·陕西模拟) 如图，在平行四边形ABCD中，对角线AC的垂直平分线分别与边AB和边CD的延长线交于点M，N，垂足为点O.求证：BM＝DN.

答案解析收藏纠错 + 选题
25. (2021·陕西模拟) 如图，四边形ABCD中，AB $\text{[math]}$ DC，AC平分∠BAD，CE $\text{[math]}$ DA交AB于点E.求证：四边形ADCE是菱形.

答案解析收藏纠错 + 选题

四、作图题

26. (2017·陕西) 如图，在钝角△ABC中，过钝角顶点B作BD⊥BC交AC于点D．请用尺规作图法在BC边上求作一点P，使得点P到AC的距离等于BP的长．（保留作图痕迹，不写作法）

答案解析收藏纠错 + 选题
27. (2021·陕西模拟) 如图，在矩形 $\text{[math]}$ 中，请利用尺规作图：分别在边 $\text{[math]}$ 、 $\text{[math]}$ 上作点 $\text{[math]}$ 、 $\text{[math]}$ ，使四边形 $\text{[math]}$ 是菱形.（不写作法保留作图痕迹）

答案解析收藏纠错 + 选题
28. (2021·陕西模拟) 如图，在 $\text{[math]}$ 中，∠A＝30°，请用尺规作图法，在AC边上求作一点M，使得AM＝2BM.（不写作法，保留作图痕迹）

答案解析收藏纠错 + 选题
29. (2021·陕西模拟) 如图，已知 $\text{[math]}$ ，请利用尺规作图法在AB上求作一点P，使得∠PAC＝∠PCA.（不写作法，保留作图痕迹）

答案解析收藏纠错 + 选题
30. (2021·陕西模拟) 如图，在△ABC中，BD是边AC上的高.请用尺规作图法，在BD上求作一点E，使得∠CED+∠ABD＝90°.（保留作图痕迹，不写作法）

答案解析收藏纠错 + 选题
31. (2021·兴平模拟) 如图，请用尺规作 $\text{[math]}$ ，使得 $\text{[math]}$ 与 BC 相切（不写作法，保留作图痕迹）

答案解析收藏纠错 + 选题
32. (2021·渭滨模拟) 如图，在△ABC中，点D为AB中点，请用尺规作图方法，在线段AC上找一点E，使得DE∥BC.（请保留作图痕记，不写作法）

答案解析收藏纠错 + 选题

五、综合题

33. (2017·陕西) 如图，已知⊙O的半径为5，PA是⊙O的一条切线，切点为A，连接PO并延长，交⊙O于点B，过点A作AC⊥PB交⊙O于点C、交PB于点D，连接BC，当∠P=30°时，
1. （1）求弦AC的长；
2. （2）求证：BC∥PA．
答案解析收藏纠错 + 选题
34. (2021·陕西模拟) 如图

[问题探究]
1. （1）如图1， $\text{[math]}$ ABC为等边三角形，边长为6，AD⊥BC，垂足为点D，点E和点F分别是线段和AD和AB上的两个动点，连接CE，EF.则CE+EF的最小值为；
2. （2）如图2，⊙O为 $\text{[math]}$ ABC的外接圆，AB是直径，AC＝BC，点D是直径AB左侧的圆上一点，连接DA，DB，DC.将 $\text{[math]}$ ACD绕点C逆时针旋转得到 $\text{[math]}$ BCE.若CD＝4，求四边形ADBC的面积；
3. （3）如图3，⊙O为等边 $\text{[math]}$ ABC的外接圆，半径为2，点D在劣弧 $\text{[math]}$ 上运动（不与点A，B重合），
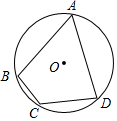
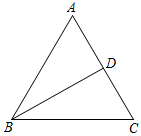
  连接DA.DB，DC.设线段DC的长为x.四边形ADBC的面积为S.
  
  ①求S与x的函数关系式；
  
  ②若点M，N分别在线段CA，CB上运动（不含瑞点），经过探究发现，点D运动到每一个确定的位置. $\text{[math]}$ DMN的周长有最小值t，随着点D的运动，t的值会发生变化.求所有t值中的最大值，并求此时四边形ADBC的面积S.
答案解析收藏纠错 + 选题
35. (2021·兴平模拟) 如图
1. （1）问题提出：
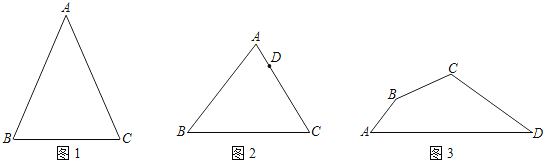
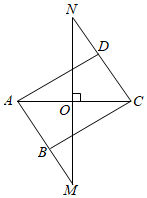
  如图1，在△ABC中，已知AB＝AC＝5，BC＝4，在BC上找一点D，使得线段AD将△ABC分成面积相等的两部分，画出线段AD，并写出AD的长为 ▲ .
2. （2）问题探究：
  如图2，点D是△ABC边AC上一定点，在BC上找一点E，使得线段DE将△ABC分成面积相等的两部分，并说明理由.
3. （3）问题解决：
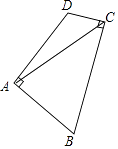
  如图3，四边形ABCD是西安市高新区新近改造过程中的一块不规则空地，为了美化环境，市规划办决定在这块地里种植两种花卉，打算过点C修一条笔直的通道，以便市民出行观赏花卉，要求通道两侧种植花卉的面积相等，经测量AB＝20米，AD＝100米，∠A＝60°，∠ABC＝150°，∠BCD＝120°，若将通道记为CF，请你画出通道CF，并求出通道CF的长.
答案解析收藏纠错 + 选题
36. (2021·兴平模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，交 $\text{[math]}$ 于点 D，过点 D 作 $\text{[math]}$ 于点 E.
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
37. (2021·兴平模拟) 如图，已知圆O的直径AB垂直于弦CD于点E，连接CO并延长交AD于点F，且CF⊥AD.
1. （1）证明：点E是OB的中点；
2. （2）若AB=8，求CD的长.
答案解析收藏纠错 + 选题

试卷信息