
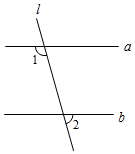


①如果a=﹣2,那么不等式组的解集是﹣2≤x<1
②如果不等式组的解集是﹣3≤x<1,那么a=﹣3
③如果不等式组的整数解只有﹣2,﹣1,0,那么a=﹣2
④如果不等式组无解,那么a≥1
其中所有正确说法的序号是( )




a.90名学生每日平均家务劳动时长的频数分布表:
|
分组 |
频数 |
|
20≤x<25 |
9 |
|
25≤x<30 |
m |
|
30≤x<35 |
15 |
|
35≤x<40 |
24 |
|
40≤x<45 |
n |
|
45≤x<50 |
9 |
|
合计 |
90 |
b.90名学生每日平均家务劳动时长频数分布直方图:

c . 每日平均家务劳动时长在35≤x<40这一组的是:
35 35 35 35 36 36 36 36 36 37 37 37
38 38 38 38 38 38 38 39 39 39 39 39
d . 小东每日平均家务劳动时长为37min .
根据以上信息,回答下列问题:

解:∵PN⊥OB于点N ,
∴∠PNB= ▲ °( )(填推理的依据)
∵PM∥OB ,
∴∠MPN=∠PNB=90°,
∠POB= ▲ ( )(填推理的依据)
∵OP平分∠AOB , 且∠AOB=60°,
∴∠POB= ∠AOB=30°(角的平分线的定义)
∴∠MPO= ▲ °.
∵∠MPO+∠OPN=∠MPN ,
∴∠OPN= ▲ °.

|
如图,AB∥CD , 点E是线段AB , CD所在直线外的一点,连接BE , DE , 探究∠BED , ∠ABE , ∠CDE之间的数量关系. |
小凯画出了图1,图2,分析思路及结论如下:
| 分析思路: 要寻求三个角之间的数量关系,根据图中角的位置特征,可以借助平行线进行角的位置的转换. 如图1,过点E作MN∥AB . ⑴由MN∥AB可知∠BEN=∠ABE; ⑵由MN∥AB , AB∥CD得到MN∥CD , 可知∠NED=∠CDE; ⑶由∠BED=∠BEN+∠NED , 得到结论:∠BED=∠ABE+∠CDE 如图2,类似图1的分析… 得到结论:∠BED+∠ABE+∠CDE=360°. |
小明认为小凯只考虑了点E在直线AB , CD之间的情况,点E的位置应该还有其他情况.
根据以上材料,解答问题:画出一种点E不在直线AB , CD之间的图形,写出探究∠BED , ∠ABE , ∠CDE之间的数量关系的分析思路及结论.
|
月份 |
销售量/件 |
销售额/元 |
|
|
冰墩墩 |
雪容融 |
||
|
第1个月 |
100 |
40 |
14800 |
|
第2个月 |
160 |
60 |
23380 |

