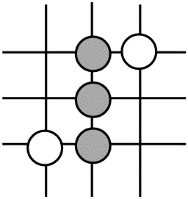
B .
B . 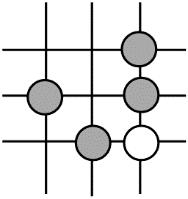
C .
C . 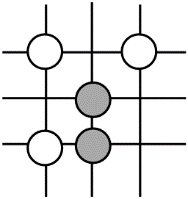
D .
D . 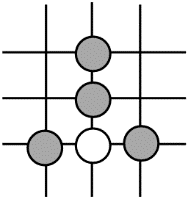
| 身高( | 1.65 | 1.68 | 1.70 | 1.72 | 1.76 | 1.80 |
| 人数 | 3 | 4 | 6 | 7 | 6 | 4 |
则这30名学生身高的众数和中位数分别是( )


| 甲 | 乙 | 丙 | 丁 | |
| | 11.5 | 11.5 | 11.6 | 11.6 |
| | 0.45 | 0.53 | 0.45 | 0.48 |
要选一位成绩优秀且发挥稳定的运动员参加奥运会预选赛,则应该选择的是.


甲组:30,60,60,60,60,60,70,90,90,100
乙组:50,50,60,70,70,80,80,80,90,90.
|
组别 |
平均分 |
中位数 |
方差 |
合格率 |
优秀率 |
|
甲组 |
68分 |
| 376 | 96% | 30% |
| 乙组 | | | 196 | 80% | 20% |
|
时间 |
节次 |
|
|
上午 |
7:30 |
到校 |
|
8:00~8:40 |
第一节 |
|
|
8:50~9:30 |
第二节 |
|
|
…… |
…… |
|


