山东省滨州市滨城区2020-2021学年八年级下学期数学期末...

更新时间：2021-08-29 浏览次数：172 类型：期末考试

一、单选题

1. 下列式子是最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. 函数 $\text{[math]}$ 中，自变量 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. 下列二次根式，化简后能与 $\text{[math]}$ 合并的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. 下列命题的逆命题成立的是（）

A . 若 $\text{[math]}$ ，则 $\text{[math]}$ B . 对顶角相等 C . 对角线互相平分的四边形是平行四边形 D . 矩形的对角线相等

答案解析收藏纠错 + 选题
6. 关于一次函数 $\text{[math]}$ ，下列说法正确的是（）

A . 图象经过点 $\text{[math]}$ B . 图象经过第三象限 C . 函数 $\text{[math]}$ 随自变量 $\text{[math]}$ 的增大而增大 D . 当 $\text{[math]}$ 时， $\text{[math]}$

答案解析收藏纠错 + 选题
7. 体育课上甲、乙两同学比赛跑步，其路程 $\text{[math]}$ （单位： $\text{[math]}$ ）与时间 $\text{[math]}$ （单位： $\text{[math]}$ ）之间的图象如图所示，下列说法错误的是（）

A . 甲、乙进行的是 $\text{[math]}$ 赛跑 B . 甲的平均速度大于乙的平均速度 C . 前 $\text{[math]}$ ，甲的速度大于乙的速度 D . 甲、乙同时到达终点

答案解析收藏纠错 + 选题
8. 某校为落实作业管理、睡眠管理、手机管理、读物管理、体质管理工作有关要求，随机抽查了部分学生每天的睡眠时间，制定如下统计表．

睡眠时间/ $\text{[math]}$

6

7

8

9

人数

10

20

15

5

则所抽查学生每天睡眠时间的平均数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 某村欲购进一批杏树，考察中随机从甲、乙、丙、丁四个品种中各选了10棵，每棵产量（单位： $\text{[math]}$ ）的平均数 $\text{[math]}$ 及方差 $\text{[math]}$ 如表所示：

统计量

甲

乙

丙

丁

$\text{[math]}$

40

40

38

38

$\text{[math]}$

1.5

2.3

1.8

2.3

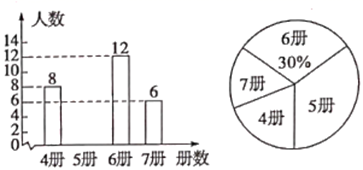
该村准备从这四个品种中选出一种产量既高又稳定的杏树，则应选的品种是（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
10. 满足下列条件时， $\text{[math]}$ 不是直角三角形的为（）

A . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 中线 $\text{[math]}$

答案解析收藏纠错 + 选题
11. 小明在做“练习使用弹簧测力计”的实验时，用 $\text{[math]}$ （单位： $\text{[math]}$ ）表示弹簧受到的拉力，用 $\text{[math]}$ （单位： $\text{[math]}$ ）表示挂上重物后弹簧的总长（在弹性范围内， $\text{[math]}$ 是 $\text{[math]}$ 一次函数）．记录实验数据如下：

$\text{[math]}$

1

2.5

3

……

$\text{[math]}$

5

8

9

……

小明得出下列结论：①弹性范围内， $\text{[math]}$ 与 $\text{[math]}$ 的关系式是 $\text{[math]}$ ；②不挂重物时弹簧的长度为 $\text{[math]}$ ；③若弹簧总长不能超过 $\text{[math]}$ ，则弹簧所受到的拉力不能超过 $\text{[math]}$ ；④弹性范围内，弹簧伸长的长度与弹簧所受拉力成正比．其中正确结论的个数是（）

A . 4 B . 3 C . 2 D . 1

答案解析收藏纠错 + 选题
12. 如图，在平面直角坐标系中，菱形ABCD的顶点A在 $\text{[math]}$ 轴上，顶点B ， C的坐标分别为(−6，0)，(4，0)，则点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2020·黑龙江) 如图，在四边形ABCD中，AD//BC，在不添加任何辅助线的情况下，请你添加一个条件，使四边形ABCD是平行四边形（填一个即可）．

答案解析收藏纠错 + 选题
15. 如图，在矩形 $\text{[math]}$ 中，对角线 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
16. 如图，在 $\text{[math]}$ 中，点 $\text{[math]}$ ， $\text{[math]}$ 分别是边 $\text{[math]}$ ， $\text{[math]}$ 的中点，点 $\text{[math]}$ 是线段 $\text{[math]}$ 上的一点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
17. 若一组数据4，x ， 5，7，9的平均数为6，则这组数据的方差为．

答案解析收藏纠错 + 选题
18. 已知正比例函数的图象过点(2，4)．把该函数图象平移，使它过点(1，−1)，则平移后所得函数的解析式是．

答案解析收藏纠错 + 选题
19. 某生态体验园推出了甲、乙两种消费卡．甲、乙两卡所需费用 $\text{[math]}$ ， $\text{[math]}$ （单位：元）与入园次数 $\text{[math]}$ （单位：次）的函数关系如图所示．当x满足时， $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. 如图，正方形ABCD中，AB=6，点E在边CD上，且DE=2．将△ADE沿AE对折至△AFE ，延长EF交BC于点G ，连接AG ， CF ．下列结论：①△ABG≌△AFG；②∠GAE=45°；③BG=GC；④AG//CF；⑤△CFE是等腰三角形，其中正确的结论有（填写所有正确结论的序号）．

答案解析收藏纠错 + 选题

三、解答题

21. 书籍是人类进行的阶梯．为了解学生的课外阅读情况，某校随机抽查了部分学生本学期阅读课外书的册数，并绘制出如下统计图．
1. （1）共抽查了多少名学生？
2. （2）请补全条形统计图，并写出被抽查学生本学期阅读课外书册数的众数、中位数；
3. （3）根据抽查结果，请估计该校1200名学生中本学期课外阅读5册书的学生人数．
答案解析收藏纠错 + 选题
22. 如图，在▱ABCD中，对角线AC与BD相交于点O ，过点O的直线EF与BA ， DC的延长线分别交于点E ， F ，连接BF ， DE ．
1. （1）求证：AE=CF；
2. （2）请添加一个条件，使四边形BFDE是菱形，并说明理由．
答案解析收藏纠错 + 选题
23. 5G时代的到来，给人类生活带来巨大变化．现有A ， B两种型号的5G手机，已知销售1部A型手机和1部B型手机共获利700元，销售6部A型手机和4部B型手机共获利3400元．
1. （1）请问1部A型手机和1部B型手机的利润分别为多少元？
2. （2）某营业厅计划购进A ， B两种型号手机共30部，其中B型手机的数量不多于A型手机数量的2倍．两种型号手机各购进多少部，全部销售后获利最大？最大利润是多少？
答案解析收藏纠错 + 选题
24. 勾股定理是人类重大科学发现之一．我国古代数学书《周髀算经》记载，约公元前11世纪，我国古代劳动人民就知道“若勾三，股四，则弦五”，比西方早500多年．请你运用学到的知识、方法和思想探究以下问题．
1. （1）（探究一）我国汉代数学家赵爽创制了“赵爽弦图”，通过图形切割、拼接，巧妙地利用面积关系证明了勾股定理．古往今来，人们对勾股定理的证明一直保持着极大的热情．意大利著名画家达·芬奇用两张一样的纸片，拼出不一样的空洞，利用空洞面积相等也成功地证明了勾股定理（如图）．
  请你写出这一证明过程（图中所有的四边形都是正方形，三角形都是直角三角形）．
2. （2）（探究二）在学习勾股定理的过程中，我们获得了以下数学活动经验：分别以直角三角形的三边为边向外侧作正方形（如图2），它们的面积 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间满足的等量关系是：．
3. （3）迁移应用：如图3，图中所有的四边形都是正方形，三角形都是直角三角形．若正方形 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的边长分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则正方形 $\text{[math]}$ 的面积是．
4. （4）（探究三）如图4，分别以直角三角形的三边为直径向外侧作半圆，则它们的面积 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间满足的等量关系是．
5. （5）迁移应用：如图5，直角三角形的两条直角边长分别为 $\text{[math]}$ ， $\text{[math]}$ ，斜边长为 $\text{[math]}$ ，分别以三边为直径作半圆．若 $\text{[math]}$ ， $\text{[math]}$ ，则图中阴影部分的面积等于．
6. （6）（探究四）《九章算术》卷九“勾股”中记载：今有立木，系索其末，委地三尺．引索却行，去本八尺而索尺．问索长几何．译文：今有一竖立着的木柱，在木桩的上端系有绳索，绳索从木柱上端顺木柱下垂后，堆在地面的部分尚有 $\text{[math]}$ 尺．牵着绳索（绳索与地面接触）退行，在距木柱根部 $\text{[math]}$ 尺处时绳索用尽．问绳索长多少？
答案解析收藏纠错 + 选题
25. 李明酷爱数学，勤于思考，善于反思．在学习八年级下册数学知识之后，他发现“二次根式、勾股定理、一次函数、平行四边形”都和“将军饮马”问题有关联，并且为解决“饮马位置”“最短路径长”等问题，提供了具体的数学方法．于是他撰写了一篇数学作文．请你认真阅读思考，帮助李明完成相关问题．
“将军饮马”问题的探究与拓展

八年级三班李明

“白日登山望烽火，黄昏饮马傍交河”（唐·李颀《古从军行》），这句诗让我想到了有趣的“将军饮马”问题：将军从 $\text{[math]}$ 地出发到河边 $\text{[math]}$ 饮马，然后再到 $\text{[math]}$ 地军营视察，怎样走路径最短？

（数学模型）如图1， $\text{[math]}$ ， $\text{[math]}$ 是直线 $\text{[math]}$ 同旁的两个定点．在直线 $\text{[math]}$ 上确定一点 $\text{[math]}$ ，使 $\text{[math]}$ 的值最小．

（问题解决）作点 $\text{[math]}$ 关于直线 $\text{[math]}$ 的对称点 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，则点 $\text{[math]}$ 即为所求．此时， $\text{[math]}$ 的值最小，且 $\text{[math]}$ ．
1. （1）（模型应用）
  问题1．如图2，经测量得 $\text{[math]}$ ， $\text{[math]}$ 两点到河边 $\text{[math]}$ 的距离分别为 $\text{[math]}$ 米， $\text{[math]}$ 米，且 $\text{[math]}$ 米．请计算出“将军饮马”问题中的最短路径长．
2. （2）问题2．如图3，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 边上，且 $\text{[math]}$ ，点 $\text{[math]}$ 是对角线 $\text{[math]}$ 上的一个动点，则 $\text{[math]}$ 的最小值是．
3. （3）问题3．如图4，在平面直角坐标系中，点 $\text{[math]}$ ，点 $\text{[math]}$ ．
  
  请在 $\text{[math]}$ 轴上确定一点 $\text{[math]}$ ，使 $\text{[math]}$ 的值最小，并求出 $\text{[math]}$ 的坐标；
4. （4）请直接写出 $\text{[math]}$ 的最小值．
5. （5）（模型迁移）
  问题4．如图5，菱形 $\text{[math]}$ 中，对角线 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．点 $\text{[math]}$ 和点 $\text{[math]}$ 分别为 $\text{[math]}$ ， $\text{[math]}$ 上的动点，求 $\text{[math]}$ 的最小值．
答案解析收藏纠错 + 选题