安徽中考数学真题模拟题分类卷6 概率与统计

更新时间：2021-12-01 浏览次数：182 类型：二轮复习

一、单选题

1. (2019·安徽) 在某时段由50辆车通过一个雷达测速点，工作人员将测得的车速绘制成如图所示的条形统计图，则这50辆车的车速的众数（单位：km/h）为（）

A . 60 B . 50 C . 40 D . 15

答案解析收藏纠错 + 选题
2. (2021·安徽模拟) 为秉承“弘扬传统文化，增强校园文化底蕴”的宗旨，某校举行“古诗词”大赛，八年级(1)班选出了6名同学参加，他们的成绩分别为90，88，85，92，90，86，则这6名同学成绩的中位数是（）

A . 92 B . 89 C . 88 D . 85

答案解析收藏纠错 + 选题
3. (2021·安徽) 如图，在三条横线和三条竖线组成的图形中，任选两条横线和两条竖线都可以围成一个矩形，从这些矩形中任选一个，则所选矩形含点A的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024八下·潘集期末) 冉冉的妈妈在网上销售装饰品．最近一周，每天销售某种装饰品的个数为：.11，10，11，13，11，13，15关于这组数据，冉冉得出如下结果，其中错误的是（）

A . 众数是11 B . 平均数是12 C . 方差是 $\text{[math]}$ D . 中位数是13

答案解析收藏纠错 + 选题
5. (2018·安徽) 为考察两名实习工人的工作情况，质检部将他们工作第一周每天生产合格产品的个数整理成甲，乙两组数据，如下表：
甲
2
6
7
7
8
乙
2
3
4
8
8
类于以上数据，说法正确的是（）

A . 甲、乙的众数相同 B . 甲、乙的中位数相同 C . 甲的平均数小于乙的平均数 D . 甲的方差小于乙的方差

答案解析收藏纠错 + 选题
6. (2016·安徽)
自来水公司调查了若干用户的月用水量x（单位：吨），按月用水量将用户分成A、B、C、D、E五组进行统计，并制作了如图所示的扇形统计图．已知除B组以外，参与调查的用户共64户，则所有参与调查的用户中月用水量在6吨以下的共有（　　）
组别
月用水量x（单位：吨）
A
0≤x＜3
B
3≤x＜6
C
6≤x＜9
D
9≤x＜12
E
x≥12

A . 18户 B . 20户 C . 22户 D . 24户

答案解析收藏纠错 + 选题
7. (2021·合肥模拟) 某数学兴趣小组为了了解本班学生一周课外阅读的时间，随机调查5名学生，并将所得数据整理如表表中有一个数字被污染而模糊不清，但曾计算得该组数据的平均数为6，则这组数据的方差和中位数分别为（）

学生编号

1

2

3

4

5

一周课外阅读时间（小时）

7

5

4

8

A . 2，6 B . 1.5，4 C . 2，4 D . 6，6

答案解析收藏纠错 + 选题
8. (2021·安徽模拟) 一个质地均匀的正四面体，四个面上分别写着数字 $\text{[math]}$ 将它投掷于桌面上，连续投掷两次，则两次与桌面接触的面上的数字之和为5的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021七下·怀安期末) 初中生骑电动车上学存在安全隐患，为了解某初中2200个学生家长对“中学生骑电动车上学”的态度，从中随机调查200个家长，结果有160个家长持反对态度，则下列说法正确的是（）

A . 调查方式是普查 B . 该校只有160个家长持反对态度 C . 样本是200个家长 D . 该校约有80%的家长持反对态度

答案解析收藏纠错 + 选题

10. (2021·包河模拟) 甲、乙两台机床生产某款新产品，前6天生产优等品的数量如表：对两台机床生产优等品数量作如下分析，其中说法正确的是（）

	第1天	第2天	第3天	第4天	第5天	第6天
甲	9	8	6	7	8	10
乙	8	7	10	7	8	8

A . 它们优等品数量的平均数不同 B . 它们优等品数量的中位数不同 C . 它们优等品数量的众数不同 D . 它们优等品数量的方差不同

答案解析收藏纠错 + 选题

11. (2021·太和模拟) 如图，四边形 $\text{[math]}$ 的对角线 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点，若在四边形 $\text{[math]}$ 内任取一点，则这一点落在图中阴影部分的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2021·怀宁模拟) 如图，随机闭合开关S₁ ， S₂ ， S₃中的两个，灯泡不能够发光的概率是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、综合题

13. (2021·休宁模拟) 今年2～4月某市出现了400名新冠肺炎患者，市委根据党中央的决定，对患者进行了免费治疗，图1是该市轻症、重症、危重症三类患者的人数分布统计图（不完整），图2是这三类患者的人均治疗费用统计图．请回答下列问题．
1. （1）轻症患者的人数是多少？
2. （2）所有患者的平均治疗费用是多少万元？
3. （3）由于部分轻症患者康复出院，为减少病房拥挤，拟对某病房中的 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 五位患者任选两位转入另一病房，请用树状图法或列表法求出恰好选中 $\text{[math]}$ 、 $\text{[math]}$ 两位患者的概率．
答案解析收藏纠错 + 选题

14. (2021·安徽) 为了解全市居民用户用电情况，某部门从居民用户中随机抽取100户进行月用电量(单位：kM·h)调查，按月用电量50～100，100～150，100～200，200～250，250～300，300～350进行分组，绘制频数分布直方图如下：

（1）求频数分布直方图中x的值；
（2）判断这100户居民用户月用电量数据的中位数在哪一组(直接写出结果)；

（3）设各组居民月平均用电量如下表：

组别	50～100	100～150	150～200	200～250	250～300	300～350
月平均用电量（单位：kM·h）	75	125	175	225	275	325

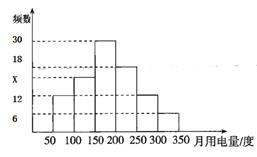
根据上述信息，估计该市居民用户月用电量的平均数.

答案解析收藏纠错 + 选题

15. (2020·安徽) 某单位食堂为全体名职工提供了 $\text{[math]}$ 四种套餐，为了解职工对这四种套餐的喜好情况，单位随机抽取 $\text{[math]}$ 名职工进行“你最喜欢哪一种套餐（必选且只选一种）”问卷调查，根据调查结果绘制了条形统计图和扇形统计图，部分信息如下：
1. （1）在抽取的240人中最喜欢A套餐的人数为，扇形统计图中“C”对应扇形的圆心角的大小为；
2. （2）依据本次调查的结果，估计全体960名职工中最喜欢B套餐的人数；
答案解析收藏纠错 + 选题

16. (2019·安徽) 为监控某条生产线上产品的质量，检测员每个相同时间抽取一件产品，并测量其尺寸，在一天的抽检结束后，检测员将测得的个数据按从小到大的顺序整理成如下表格：

编号	①	②	③	④	⑤	⑥	⑦	⑧	⑨	⑩	⑪	⑫	⑬	⑭	⑮
尺寸（cm）	8.72	8.88	8.92	8.93	8.94	8.96	8.97	8.98	a	9.03	9.04	9.06	9.07	9.08	b

按照生产标准，产品等次规定如下：

尺寸（单位：cm）	产品等次
8.97≤x≤9.03	特等品
8.95≤x≤9.05	优等品
8.90≤x≤9.10	合格品
x＜8.90或x＞9.10	非合格品

注：在统计优等品个数时，将特等品计算在内；在统计合格品个数时，将优等品（含特等品）仅算在内.

（1）已知此次抽检的合格率为80%，请判断编号为⑮的产品是否为合格品，并说明理由
（2）已知此次抽检出的优等品尺寸的中位数为9cm.
（i）求a的值，

（ii）将这些优等品分成两组，一组尺寸大于9cm，另一组尺寸不大于9cm，从这两组中各随机抽取1件进行复检，求抽到的2件产品都是特等品的概率.

答案解析收藏纠错 + 选题

17. (2020·乌兰浩特模拟) “校园诗歌大赛”结束后，张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理，并分别绘制成扇形统计图和频数直方图部分信息如下：
1. （1）本次比赛参赛选手共有人，扇形统计图中“69.5～79.5”这一组人数占总参赛人数的百分比为；
2. （2）赛前规定，成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分，试判断他能否获奖，并说明理由；
3. （3）成绩前四名是2名男生和2名女生，若从他们中任选2人作为获奖代表发言，试求恰好选中1男1女的概率.
答案解析收藏纠错 + 选题
18. (2016·安徽) 一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字，分别是1，4，7，8．现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数．
1. （1）写出按上述规定得到所有可能的两位数；
2. （2）从这些两位数中任取一个，求其算术平方根大于4且小于7的概率．
答案解析收藏纠错 + 选题
19. (2021·合肥模拟) 某校数学社团对该校学生进行“舌尖上的合肥——我最喜爱的合肥小吃”随机调查，每人只能从中“ $\text{[math]}$ ．锅贴、 $\text{[math]}$ ．鸡蛋灌饼、 $\text{[math]}$ ．小笼包、 $\text{[math]}$ ．赤豆糊”中选择一个本人最喜欢的小吃．将调查问卷整理后绘制了如下两幅不完整的统计图．请结合统计图中的信息，解决下列问题：
　
1. （1）小笼包所在扇形的圆心角的度数为 $\text{[math]}$ ，将条形统计图补充完整；
2. （2）该校共有1200名同学，估计最喜欢赤豆糊的同学有名；
3. （3）甲、乙两个同学从这四种小吃：“ $\text{[math]}$ ．锅贴、 $\text{[math]}$ ．鸡蛋灌饼、 $\text{[math]}$ 小笼包、 $\text{[math]}$ ．赤豆糊”中随机地选一项去品尝，请你利用树状图或表格，求出两位同学选到 $\text{[math]}$ 、 $\text{[math]}$ 小吃的概率．
答案解析收藏纠错 + 选题

20. (2021·安徽模拟) 国内生产总值（GDP）是衡量国家（或地区）经济状况的最佳指标，根据安徽省统计局发布的2021年一季度安徽各市GDP统计数据结果，现把GDP值用m亿元表示，并将其GDP分成了A $\text{[math]}$ 、B $\text{[math]}$ 、C $\text{[math]}$ 、D $\text{[math]}$ 四个等级，其中GDP由高到低前五名分别是合肥2356.3亿元，芜湖995.68亿元，滁州759.8亿元，阜阳694.8亿元，安庆597.2亿元，根据调查结果绘制了统计表和扇形统计图，部分信息如下：

等级	GDP值区间	频数
A	100≤m＜300	4
B	300≤m＜500	c
C	500≤m＜700	5
D	m≥700	d

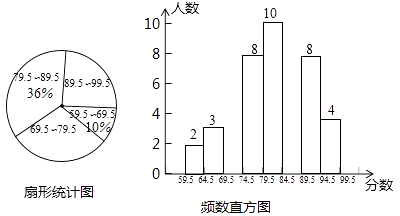
请根据图表中提供的信息，回答下列问题：

（1） a=，b= ，c=，d=；
（2）某同学来自以上地区中的某一城市，他知道自己所在城市2021年一季度的GDP值，若他想知道自己所在城市2021年一季度GDP是否处于中上游，他需要知道什么统计量，请说明理由；
（3）若从GDP值不低于700亿元的城市中任选两个，了解其近两年GDP值的变化情况，求同时选中合肥和芜湖的概率．

答案解析收藏纠错 + 选题

21. (2021·安徽模拟) 育英中学组织了一次“学中华文化经典知识竞赛”活动，从全校参赛的800名学生中抽取80名学生，将其成绩(满分100分，取整数)分成40~50，50~60，60~70，70~80，80~90，90~100(下限数据包括在本组中，如40属于第一小组)六个小组后画出如图所示的不完整的频数分布直方图．观察图中信息，回答下列问题：
1. （1）求第六小组的频率；
2. （2）估计该校参赛学生中成绩在80分及以上的人数；
3. （3）在抽取的80名学生中，成绩在90分及以上的学生中九年级学生有3人，其余都为八年级学生，现要在成绩在90分及以上的学生中随机抽取两名学生对其他学生进行中华文化经典知识宣讲，求抽到的两名学生都是九年级学生的概率。
答案解析收藏纠错 + 选题
22. (2021·安徽模拟) 本周末校园专场招聘会，某大学金融学院200名学生参加某国有银行的甲、乙、丙三个部门的定向招聘（每个人都参加了报名，每人都只能报一个部门），他们到各个部门报名人数百分比所对应的圆心角如图（部门录取人数÷部门报名人数）×100%

部门

甲

乙

丙

录取率

30%

40%

60%
1. （1）到乙部门报名人数有人，甲部门的录取人数为人，该企业的总体录取率为%．
2. （2）如果到甲部门报名的人员中有一些人员改到丙部门报名，在保持各部门录取率不变的情况下，该企业的总体录取率恰好增加6%，问有多少人从甲部门改到丙部门报名？
3. （3） 3位好同学：小明，小强，小刚分别报名甲、乙、丙三个部门，均被录取，辅导员将三封该企业录取通知（信封外表完全一样）混在一起交给他们三人，他们同时打开，请问他们三人同时打开恰好都属于自己的录取通知的概率是多少？
答案解析收藏纠错 + 选题
23. (2021·包河模拟) 某校为了解七、八年级学生对“新冠疫情”防护知识的掌握情况，从七、八年级各随机抽取30名学生进行测试，并对成绩（百分制）进行整理、描述和分析．部分信息如下：
①七年级成绩频数分布直方图（每组含最小值，不含最大值，最后一组含100分）；

②七年级在 $\text{[math]}$ 这一组的成绩是：78，74，76，78，77，79；

③七、八年级抽取学生成绩的平均数、中位数如下：

年级

平均数

中位数

七

74.8

$\text{[math]}$

八

75.4

78.5

根据以上信息，回答下列问题：
1. （1）在这次测试中，七年级在70分以上（含70分）的有人；表中a的值为；
2. （2）求七年级成绩在 $\text{[math]}$ 这一组的6个人成绩的方差；
3. （3）参加测试的七年级小静同学说：“我和八年级的小蓓都是77分，但我在七年级抽取的同学中排名更靠前．”八年级小蓓同学说：“虽然我不知道其他人的分数，但我的分数是77分，比平均分高，所以我的成绩一定是八年级抽取同学中的前15名．”请你对这两种说法是否符合题意进行判断，并加以说明．
答案解析收藏纠错 + 选题
24. (2021·怀宁模拟) 随着智能手机的普及率越来越高以及移动支付的快捷高效性，中国移动支付在世界处于领先水平，为了解人们平时最喜欢用哪种移动支付方式，因此在某步行街对行人进行随机抽样调查，以下是根据调查结果分别整理的不完整的统计表和统计图．

移动支付方式

支付宝

微信

其他

人数/人

200

90

请你根据上述统计表和统计图提供的信息．完成下列问题：
1. （1）在此次调查中，使用支付宝支付的人数为人，表示微信支付的扇形所对的圆心角度数为度．
2. （2）某天该步行街人流量为3万人，其中80%的人购物并选择移动支付，请你依据此次调查获得的信息估计一下当天使用微信支付的人数．
3. （3）甲、乙、丙三人都只习惯使用支付宝和微信支付，并且他们选择这两种支付的可能性是相同的，请计算三人恰好选择同一种支付方式的概率．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

安徽中考数学真题模拟题分类卷6 概率与统计

副标题：

*注意事项：

安徽中考数学真题模拟题分类卷6 概率与统计

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

组别	月用水量x（单位：吨）
A	0≤x＜3
B	3≤x＜6
C	6≤x＜9
D	9≤x＜12
E	x≥12

学生编号	1	2	3	4	5
一周课外阅读时间（小时）	7	5	4		8

部门	甲	乙	丙
录取率	30%	40%	60%

年级	平均数	中位数
七	74.8	$\text{[math]}$
八	75.4	78.5

移动支付方式	支付宝	微信	其他
人数/人		200	90