备考2022年中考数学一轮复习（湘教版）专题67 数据的分析

更新时间：2021-10-08 浏览次数：120 类型：一轮复习

一、单选题

1. (2021·柳州) 某校九年级进行了3次数学模拟考试，甲、乙、丙三名同学的平均分为及方差 $\text{[math]}$ 如右表所示，那么这三名同学数学成绩最稳定的是（）

甲

乙

丙

$\text{[math]}$

91

91

91

$\text{[math]}$

6

24

54

A . 甲 B . 乙 C . 丙 D . 无法确定

答案解析收藏纠错 + 选题
2. (2021·盘锦) 甲、乙、丙、丁四人10次随堂测验的成绩如图所示，从图中可以看出这10次测验平均成绩较高且较稳定的是（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
3. (2024七下·平南期末) 全民反诈，刻不容缓！陈科同学参加学校举行的“防诈骗”主题演讲比赛，五位评委给出的分数分别为90，80，86，90，94，则这组数据的中位数和众数分别是（）

A . 80，90 B . 90，90 C . 86，90 D . 90，94

答案解析收藏纠错 + 选题
4. (2024九下·深圳模拟) 为了向建党一百周年献礼，我市中小学生开展了红色经典故事演讲比赛.某参赛小组6名同学的成绩（单位：分）分别为：85，82，86，82，83，92.关于这组数据，下列说法错误的是（）

A . 众数是82 B . 中位数是84 C . 方差是84 D . 平均数是85

答案解析收藏纠错 + 选题
5. (2021·鄂尔多斯) 小明收集了鄂尔多斯市某酒店2021年3月1日～3月6日每天的用水量（单位：吨），整理并绘制成如图所示的折线统计图，下列结论正确的是（）

A . 平均数是 $\text{[math]}$ B . 众数是10 C . 中位数是8.5 D . 方差是 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022八下·丰润期末) 某校健美操队共有10名队员，统计队员的年龄情况，结果如下：13岁3人，14岁5人，15岁2人该健美操队队员的平均年龄为（）

A . 14.2岁 B . 14.1岁 C . 13.9岁 D . 13.7岁

答案解析收藏纠错 + 选题
7. (2024九下·石家庄模拟) 一组数据：2，4，4，4，6，若去掉一个数据4，则下列统计量中发生变化的是（）

A . 众数 B . 中位数 C . 平均数 D . 方差

答案解析收藏纠错 + 选题

8. (2023·长沙模拟) 为迎接中国共产党建党一百周年，某班50名同学进行了党史知识竞赛，测试成绩统计如下表，其中有两个数据被遮盖．

成绩/分	91	92	93	94	95	96	97	98	99	100
人数	■	■	1	2	3	5	6	8	10	12

下列关于成绩的统计量中，与被遮盖的数据无关的是（）

A . 平均数，方差 B . 中位数，方差 C . 中位数，众数 D . 平均数，众数

答案解析收藏纠错 + 选题

9. (2024九上·广州开学考) 一组数据：3，4，4，4，5，若去掉一个数据4，则下列统计量中发生变化的是（）

A . 众数 B . 中位数 C . 平均数 D . 方差

答案解析收藏纠错 + 选题
10. (2024九下·南沙模拟) 为了保护环境加强环保教育，某中学组织学生参加义务收集废旧电池的活动，下面是随机抽取40名学生对收集废旧电池的数量进行的统计：

废旧电池数/节

4

5

6

7

8

人数/人

9

11

11

5

4

请根据学生收集到的废旧电池数，判断下列说法正确的是（）

A . 样本为40名学生 B . 众数是11节 C . 中位数是6节 D . 平均数是5.6节

答案解析收藏纠错 + 选题

二、填空题

11. (2021九上·南宁开学考) 为庆祝中国共产党建党一百周年，某校开展了主题为“我身边的共产党员”的演讲比赛.比赛从演讲内容、演讲技巧、演讲效果三个方面打分，最终得分按4：3：3的比例计算.若选手甲在演讲内容、演讲技巧、演讲效果三个方面的得分分别为95分、80分、90分，则选手甲的最终得分为分.

答案解析收藏纠错 + 选题
12. (2022七下·北海期末) 为了庆祝中国共产党成立100周年，某校举行“党在我心中”演讲比赛，评委将从演讲内容，演讲能力，演讲效果三个方面给选手打分，各项成绩均按百分制计，然后再按演讲内容占50%，演讲能力占40%，演讲效果占10%，计算选手的综合成绩（百分制）.小婷的三项成绩依次是84，95，90，她的综合成绩是.

答案解析收藏纠错 + 选题
13. (2021·河南) 某外贸公司要出口一批规格为 $\text{[math]}$ 克/盒的红枣，现有甲、乙两个厂家提供货源，它们的价格相同，品质也相近.质检员从两厂的产品中各随机抽取 $\text{[math]}$ 盒进行检测，测得它们的平均质量均为 $\text{[math]}$ 克，每盒红枣的质量如图所示，则产品更符合规格要求的厂家是.（填“甲”或“乙”）

答案解析收藏纠错 + 选题

14. (2022·衢州模拟) 甲乙两班举行一分钟跳绳比赛，参赛学生每分钟跳绳次数的统计结果如表：

班级	参加人数	中位数	方差	平均数
甲	45	109	181	110
乙	45	111	108	110

某同学分析如表后得到如下结论：①甲，乙两班学生平均成绩相同；②乙班优秀人数多于甲班优秀人数（每分钟跳绳≥110次为优秀）；③甲班成绩的波动比乙班大，则正确结论的序号是．

答案解析收藏纠错 + 选题

15. (2021·常德) 在某次体育测试中，甲、乙两班成绩的平均数、中位数、方差如下表所示，规定学生个人成绩大于90分为优秀，则甲、乙两班中优秀人数更多的是班.

	人数	平均数	中位数	方差
甲班	45	82	91	19.3
乙班	45	87	89	5.8

答案解析收藏纠错 + 选题

16. (2021·杭州) 现有甲、乙两种糖果的单价与千克数如下表所示

甲种糖果

乙种糖果

单价(元/千克)

30

20

千克数

2

3

将这2千克甲种糖果盒3千克乙种糖果混合成5千克什锦糖果，若商家用加权平均数来确定什锦糖果的单价，则这5千克什锦糖果的单价为元/千克

答案解析收藏纠错 + 选题
17. (2024八下·无棣月考) 已知一组数据0，1，x，3，6的平均数是y，则y关于x的函数解析式是．

答案解析收藏纠错 + 选题
18. (2022七下·大庆期末) 某人5次射击命中的环数分别为5，10，7，x ， 10，若这组数据的中位数为8，则这组数据的方差为．

答案解析收藏纠错 + 选题
19. (2024八下·海淀月考) 有甲､乙两组数据，如表所示：

甲

11

12

13

14

15

乙

12

12

13

14

14

甲､乙两组数据的方差分别为 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ （填“＞”，“＜”或“＝”）．

答案解析收藏纠错 + 选题
20. (2022·临汾模拟) 某学校八年级（2）班有20名学生参加学校举行的“学党史、看红书”知识竞赛，成绩统计如图．这个班参赛学生的平均成绩是．

答案解析收藏纠错 + 选题

三、解答题

21. (2021八上·揭西期末) 某校20名男子足球运动员的年龄情况如下表：

年龄/岁

14

15

16

17

人数

5

7

5

3

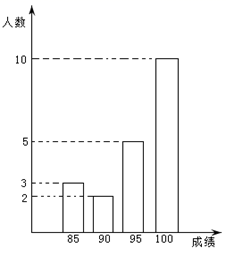
请根据表中的数据，求该20名足球运动员的年龄的众数、中位数和平均数．

答案解析收藏纠错 + 选题
22. (2017·德州模拟) 阅读后填空：某家灯具厂为了比较甲、乙两种灯的使用寿命，各抽出8支做试验，结果如下（单位：小时）．
甲：457，438，460，443，464，459，444，451；
乙：466，455，467，439，459，452，464，438．
试说明哪种灯的使用寿命长？哪种灯的质量比较稳定？

答案解析收藏纠错 + 选题
23. 我校为了纪念“一二•九”举办了八年级红歌合唱比赛，为了保证这次比赛的公正性，规定：参赛班级的基本素养、精神面貌、服装三项打分分别按5：3：2的比例计入总评成绩．二班、三班、五班的基本素养、精神面貌、服装的打分如下表，计算哪个班是第一名？
基本素养
精神面貌
服装
二班
90
96
93
三班
90
90
96
五班
96
94
90

答案解析收藏纠错 + 选题

四、综合题

24. (2021·温州) 某校将学生体质健康测试成绩分为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 四个等级，依次记为4分，3分，2分，1分.为了解学生整体体质健康状况，拟抽样进行统计分析.
1. （1）以下是两位同学关于抽样方案的对话：
  小红：“我想随机柚取七年级男、女生各60人的成绩.”
  
  小明：“我想随机柚取七、八、九年级男生各40人的成绩.”
  
  根据右侧学校信息，请你简要评价小红、小明的抽样方案.
  
  如果你来抽取120名学生的测试成绩，请给出抽样方案.
  
  学校共有七、八、九三个年级学生近千人，各段人数相近，每段男、女生人数相当，
  
  .....
2. （2）现将随机抽取的测试成绩整理并绘制成如下统计图，请求出这组数据的平均数、中位数和众数.
  某校部分学生体质健康测试成绩统计图
答案解析收藏纠错 + 选题
25. (2021·大庆) 某校要从甲，乙两名学生中挑选一名学生参加数学竞赛，在最近的8次选拔赛中，他们的成绩（成绩均为整数，单位：分）如下：
甲：92，95，96，88，92，98，99，100

乙：100，87，92，93，9▆，95，97，98

由于保存不当，学生乙有一次成绩的个位数字模糊不清，
1. （1）求甲成绩的平均数和中位数；
2. （2）求事件“甲成绩的平均数大于乙成绩的平均数”的概率；
3. （3）当甲成绩的平均数与乙成绩的平均数相等时，请用方差大小说明应选哪个学生参加数学竞赛．
答案解析收藏纠错 + 选题
26. (2021九上·南京月考) 某中学九年级学生共进行了五次体育模拟测试，已知甲、乙两位同学五次模拟测试成绩的总分相同，小明根据甲同学的五次测试成绩绘制了尚不完整的统计表，并给出了乙同学五次测试成绩的方差的计算过程.
甲同学五次体育模拟测试成绩统计表

次数

第一次

第二次

第三次

第四次

第五次

成绩（分）

35

39

37

$\text{[math]}$

40

小明将乙同学五次模拟测试成绩直接代入方差公式，计算过程如下：

$\text{[math]}$

根据上述信息，完成下列问题：
1. （1） a的值是；
2. （2）根据甲、乙两位同学这五次模拟测试成绩，你认为谁的体育成绩更好？并说明理由；
3. （3）如果甲再测试1次，第六次模拟测试成绩为38分，与前5次相比，甲6次模拟测试成绩的方差.（填“变大”“变小”或“不变”）
答案解析收藏纠错 + 选题
27. (2021九上·淮安期末) 为了从小华和小亮两人中选拔一人参加射击比赛，现对他们的射击水平进行测试，两人在相同条件下各射击6次，命中的环数如下（单位：环）：
小华：7，8，7，8，9，9；小亮：5，8，7，8，10，10.
1. （1）填写下表：
  
  平均数（环）
  
  中位数（环）
  
  方差（环²）
  
  小华
  
  8
  
  小亮
  
  8
  
  3
2. （2）根据以上信息，你认为教练会选择谁参加比赛，理由是什么？
3. （3）若小亮再射击2次，分别命中7环和9环，则小亮这8次射击成绩的方差.（填“变大”、“变小”、“不变”）
答案解析收藏纠错 + 选题

28. (2020九上·滦南期末) 某公司销售部有营业员15人，该公司为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励，为了确定一个适当的月销售目标，公司有关部门统计了这15人某月的销售量，如下表所示：

月销售量/件数	1770	480	220	180	120	90
人数	1	1	3	3	3	4

（1）直接写出这15名营业员该月销售量数据的平均数、中位数、众数；

（2）如果想让一半左右的营业员都能达到月销售目标，你认为（1）中的平均数、中位数、众数中，哪个最适合作为月销售目标？请说明理由．

温馨提示：确定一个适当的月销售目标是一个关键问题；如果目标定得太高，多数营业员完不成任务，会使营业员失去信心；如果目标定得太低，不能发挥营业员的潜力．

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

备考2022年中考数学一轮复习（湘教版）专题67 数据的分析

副标题：

*注意事项：

备考2022年中考数学一轮复习（湘教版）专题67 数据的分析

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

	基本素养	精神面貌	服装
二班	90	96	93
三班	90	90	96
五班	96	94	90

次数	第一次	第二次	第三次	第四次	第五次
成绩（分）	35	39	37	$\text{[math]}$	40

	平均数（环）	中位数（环）	方差（环²）
小华		8
小亮	8		3

废旧电池数/节	4	5	6	7	8
人数/人	9	11	11	5	4

	甲种糖果	乙种糖果
单价(元/千克)	30	20
千克数	2	3

年龄/岁	14	15	16	17
人数	5	7	5	3