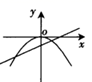
 B .
B .  C .
C .  D .
D . 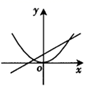

①一次函数 的图象与线段
无公共点;
②当 时,一次函数
的图象与线段
无公共点;
③当 时,反比例函数
的图象与线段
无公共点;
④当 时,二次函数
的图象与线段
无公共点.
上述说法中正确的是.

|
x |
… |
-2 |
-1 |
0 |
1 |
2 |
… |
|
y=ax2+bx+c |
… |
t |
m |
-2 |
-2 |
n |
… |
根据以上列表,回答下列问题:



①求Q点的纵坐标(用含a的式子表示);
②若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.
