山东省青岛三十九中2021-2022学年九年级上学期数学第一...

更新时间：2021-11-29 浏览次数：103 类型：月考试卷

一、单选题

1. (2024九上·成都月考) 下列方程是一元二次方程的是（）

A . （x²+3）²＝9 B . ax²+bx+c＝0 C . x²+3＝0 D . x²+ $\text{[math]}$ ＝4

答案解析收藏纠错 + 选题
2. (2021九上·青岛月考) 一元二次方程 $\text{[math]}$ 的根的情况是（）

A . 有一个实数根 B . 没有实数根 C . 有两个相等的实数根 D . 有两个不相等的实数根

答案解析收藏纠错 + 选题
3. (2021九上·青岛月考) 观察下列表格，估计一元二次方程x²＋3x－5＝0的正数解在（）

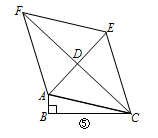
x

－1

0

1

2

3

4

x²＋3x－5

－7

－5

－1

5

13

23

A . －1和0之间 B . 0和1之间 C . 1和2之间 D . 2和3之间

答案解析收藏纠错 + 选题
4. (2021九上·青岛月考) 下列命题中，真命题是（）

A . 对角线相等的四边形是矩形 B . 对角线互相垂直的四边形是菱形 C . 对角线互相平分的四边形不一定是平行四边形 D . 对角线互相垂直平分且相等的四边形一定是正方形

答案解析收藏纠错 + 选题
5. (2023九上·市南区月考) 在一个四边形ABCD中依次连接各边的中点得到的四边形是矩形，则对角线AC与BD需要满足的条件是（）

A . 垂直 B . 相等 C . 垂直且相等 D . 不再需要条件

答案解析收藏纠错 + 选题
6. (2021九上·青岛月考) 已知已知 $\text{[math]}$ 、 $\text{[math]}$ 是一元二次方程 $\text{[math]}$ 的两根，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·高州模拟) 如图，在三角形ABC中，AB＝AC，BC＝6，三角形DEF的周长是7，AF⊥BC于F，BE⊥AC于E，且点D是AB的中点，则AF＝（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 7

答案解析收藏纠错 + 选题
8. (2022·滨州模拟) 如图，在矩形ABCD中，O为AC中点， $\text{[math]}$ 交AB于E，点G是AE中点且∠AOG＝30°，下列结论：（1）DC＝3OG；（2）OG＝ $\text{[math]}$ BC；（3） $\text{[math]}$ 等边三角形；（4）S_△AOE＝ $\text{[math]}$ S_矩形ABCD ，正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

9. (2021九上·成都期中) 方程x²＝x的解为．

答案解析收藏纠错 + 选题
10. (2021九上·千山期中) 若a是方程x²+x﹣1＝0的根，则代数式2022﹣3a²﹣3a的值是 .

答案解析收藏纠错 + 选题
11. (2024八下·龙口期末) 某工厂一月份生产机器100台，计划二、三月份共生产机器250台，设二、三月份的平均增长率为x，则根据题意列出方程是．

答案解析收藏纠错 + 选题
12. (2021九上·青岛月考) 如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DH⊥AB于点H，连接OH，若OA＝6，S_菱形ABCD＝48，则OH的长为．

答案解析收藏纠错 + 选题
13. (2021九上·青岛月考) 小明用四根长度相同的木条制作了能够活动的菱形学具，他先活动学具成为图1所示菱形，并测得 $\text{[math]}$ ，接着活动学具成为图2所示正方形，并测得正方形的对角线 $\text{[math]}$ ，则图1中对角线AC的长为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2021九上·青岛月考) 如图，在矩形ABCD中，AC、BD相交于点O，AE平分∠BAD，交BC于B，已知∠EAO＝15°，AC＝6，那么△BOE的面积为．

答案解析收藏纠错 + 选题
15. (2021九上·青岛月考) 关于x的一元二次方程(a＋1)x²－2x＋3＝0有实数根，则整数a的最大值是.

答案解析收藏纠错 + 选题
16. (2021九上·青岛月考) 如图，矩形ABCD中，AB＝6，BC＝8，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处，当△CEB′为直角三角形时，BE的长为．

答案解析收藏纠错 + 选题

三、解答题

17. (2021九上·青岛月考) 尺规作图
在三角形内做一个最大的菱形，使A为菱形的一个内角．

答案解析收藏纠错 + 选题
18. (2021九上·青岛月考) 解方程．
1. （1） x²﹣2x﹣4＝0（用配方法）；
2. （2） 2x²+3x﹣1＝0（用公式法）；
3. （3） 3x+6＝（x+2）²；
4. （4） 9（x+1）²＝4（2x﹣1）² ．
答案解析收藏纠错 + 选题
19. (2022九上·成都月考) 已知关于x的一元二次方程 $\text{[math]}$ 有两个不相等的实数根.
1. （1）求k的取值范围；
2. （2）若方程的两个不相等实数根是a，b，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
20. (2021九上·青岛月考) 如图，用长为22米的篱笆，一面利用墙（墙的最大可用长度为14米），围成中间隔有一道篱笆的长方形花圃，为了方便出入，在建造篱笆花圃时，在BC上用其他材料做了宽为1米的两扇小门．
1. （1）设花圃的一边AB长为x米，请你用含x的代数式表示另一边AD的长为米；
2. （2）若此时花圃的面积刚好为45m² ，求此时花圃的长与宽．
答案解析收藏纠错 + 选题
21. (2021九上·青岛月考) 某商店经销甲、乙两种商品．现有如下信息：

请根据以上信息，解答下列问题：
1. （1）甲、乙两种商品的零售单价分别为元和元．（直接写出答案）
2. （2）该商店平均每天卖出甲商品500件和乙商品1200件．经调查发现，甲种商品零售单价每降0.1元，甲种商品每天可多销售100件．为了使每天获取更大的利润，商店决定把甲种商品的零售单价下降m（m＞0）元．在不考虑其他因素的条件下，当m定为多少时，才能使商店每天销售甲、乙两种商品获取的利润共1700元？
答案解析收藏纠错 + 选题
22. (2021九上·青岛月考) 如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC，且DE＝ $\text{[math]}$ AC，连接CE、OE，连接AE交OD于点F.
1. （1）求证：OE＝CD；
2. （2）若菱形ABCD的边长为8，∠ABC＝60°，求AE的长.
答案解析收藏纠错 + 选题
23. (2021九上·青岛月考) 定义：有一组对角是直角的四边形叫做“准矩形”；有两组邻边（不重复）相等的四边形叫做“准菱形”．如图①，在四边形ABCD中，若∠A＝∠C＝90°，则四边形ABCD是“准矩形”；如图②，在四边形ABCD中，若AB＝AD，BC＝DC，则四边形ABCD是“准菱形”．
1. （1）如图，在边长为1的正方形网格中，A、B、C在格点（小正方形的顶点）上，请分别在图③、图④中画出“准矩形”ABCD和“准菱形”ABCD′．（要求：D、D′在格点上）；
2. （2）下列说法正确的有；（填写所有符合题意结论的序号）
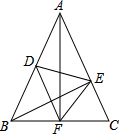
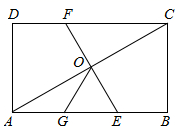
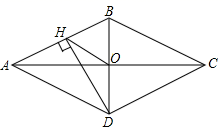
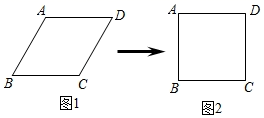
  ①一组对边平行的“准矩形”是矩形；②一组对边相等的“准矩形”是矩形；
  
  ③一组对边相等的“准菱形”是菱形；④一组对边平行的“准菱形”是菱形．
3. （3）如图⑤，在△ABC中，∠ABC＝90°，以AC为一边向外作“准菱形”ACEF，且AC＝EC，AF＝EF，AE、CF交于点D．
  ①若∠ACE＝∠AFE，求证：“准菱形”ACEF是菱形；
  
  ②在①的条件下，连接BD，若BD＝，∠ACB＝15°，∠ACD＝30°，请直接写出四边形ACEF的面积．
答案解析收藏纠错 + 选题
24. (2021九上·新津月考) 如图，平面直角坐标系中，直线l分别交x轴、y轴于A、B两点（OA＜OB）且OA、OB的长分别是一元二次方程 $\text{[math]}$ 的两个根，点C在x轴负半轴上，
且AB：AC=1：2
1. （1）求A、C两点的坐标；
2. （2）若点M从C点出发，以每秒1个单位的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，写出S关于t的函数关系式，并写出自变量的取值范围；
3. （3）点P是y轴上的点，在坐标平面内是否存在点Q，使以 A、B、P、Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题