江西省赣州市赣县区2019-2020学年九年级上学期期末数学...

更新时间：2024-07-13 浏览次数：89 类型：期末考试

一、单选题

1. (2019九上·赣州期末) 事件：“在只装有2个白球和5个黑球的袋子里，摸出一个红球”是（）

A . 可能事件 B . 随机事件 C . 不可能事件 D . 必然事件

答案解析收藏纠错 + 选题
2. (2023八下·大兴期末) 下列图案中，不是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2019九上·赣州期末) 如图，AB是半圆O的直径，∠BAC＝40°，则∠D的度数是（）

A . 140° B . 130° C . 120° D . 110°

答案解析收藏纠错 + 选题
4. (2019九上·赣州期末) 若x₁、x₂是x²+x﹣1＝0方程的两个不相等的实数根，则x₁+x₂﹣x₁x₂的值为（）

A . $\text{[math]}$ +1 B . $\text{[math]}$ ﹣2 C . ﹣2 D . 0

答案解析收藏纠错 + 选题
5. (2022九上·大余期末) 抛物线y＝x²＋4x＋3是由某个抛物线向左平移1个单位长度，再向下平移2个单位长度得到的，则原抛物线的解析式为（）

A . y＝（x－2）²＋5 B . y＝（x＋2）²－1 C . y＝（x＋1）²＋1 D . y＝（x－1）²＋1

答案解析收藏纠错 + 选题
6. (2019九上·赣州期末) 在平面直角坐标系中，若点E关于M的对称点为F，则点M是线段EF的中点．如图，已知A（1，﹣1），B（﹣1，﹣1），C（0，1），点P（0，2）关于A的对称点为P₁ ， P₁关于B的对称点为P₂ ， P₂关于C的对称点为P₃ ， P₃关于A的对称点为P₄ ， …，则点P₂₀₁₉的坐标是（）

A . （4，0） B . （﹣2，2） C . （2，﹣4） D . （﹣4，2）

答案解析收藏纠错 + 选题

二、填空题

7. (2019九上·赣州期末) 已知 $\text{[math]}$ 是关于 $\text{[math]}$ 的方程 $\text{[math]}$ 的一个根，则 $\text{[math]}$

答案解析收藏纠错 + 选题

8. (2023九上·钦州期末) 某毛绒玩具厂对一批毛绒玩具进行质量抽检，相关数据如下：

抽取的毛绒玩具数 $\text{[math]}$	20	50	100	200	500	1000	1500	2000
优等品的频数 $\text{[math]}$	19	47	91	184	462	921	1379	1846
优等品的频率 $\text{[math]}$	0.950	0.940	0.910	0.920	0.924	0.921	0.919	0.923

从这批玩具中，任意抽取的一个毛绒玩具是优等品的概率的估计值是.（精确到 $\text{[math]}$

答案解析收藏纠错 + 选题

9. (2019九上·赣州期末) 如图，把△ABC绕点C顺时针旋转35°得到△A′B′C，A′B′交AC于点D，若A′D＝CD，则∠A＝度．

答案解析收藏纠错 + 选题
10. (2022九上·桐庐月考) 某工厂2017年产品的产量为100吨，该产品产量的年平均增长率为x（x＞0），设2019年该产品的产量为y吨，则y关于x的函数关系式为．

答案解析收藏纠错 + 选题
11. (2023·黑龙江模拟) 已知圆锥的母线长为 $\text{[math]}$ 高为 $\text{[math]}$ 则该圆锥侧面展开图的圆心角是．

答案解析收藏纠错 + 选题
12. (2021九上·石城期末) 已知矩形ABCD中，AB＝8，AD＝16，将它围绕顶点A逆时针旋转一周，旋转过程中B、C、D的对应点依次为E、F、G，连接DE，则当△ADE为直角三角形时，旋转角α（0°＜α＜360°）的大小为．

答案解析收藏纠错 + 选题

三、解答题

13. (2019九上·赣州期末) 解方程：x²﹣4x＝0．

答案解析收藏纠错 + 选题
14. (2019九上·赣州期末) 如图，已知弓形的弦长AB＝12，弓高CD＝2（CD⊥AB并经过圆心O）．求弓形所在⊙O的半径的长．

答案解析收藏纠错 + 选题
15. (2019九上·赣州期末) 已知，在同一平面直角坐标系中，正比例函数y＝﹣2x与二次函数y＝﹣x²+2x+c的图象交于点A（﹣1，m）．
1. （1）求m，c的值；
2. （2）求二次函数图象的对称轴和顶点坐标．
答案解析收藏纠错 + 选题
16. (2019九上·赣州期末) 一个不透明的口袋里装有分别标有汉字“幸”、“福”、“赣”、“县”的四个小球，除汉字不同之外，小球没有任何区别．
1. （1）若从袋中任取一个球，球上的汉字刚好是“福”的概率为；
2. （2）若同时从袋中任取两个球，记取出的两个球上的汉字恰能组成“幸福”或“赣县”为事件A，请用列表或画树状图的方法求出事件A的概率．
答案解析收藏纠错 + 选题
17. (2019九上·赣州期末) 如图， $\text{[math]}$ 是 $\text{[math]}$ 中不过圆心的一条弦，请仅用无刻度的直尺，分别按下列要求画图．
1. （1）在图1中画出一条弦 $\text{[math]}$ 使 $\text{[math]}$ ；
2. （2）在图2中， $\text{[math]}$ 是 $\text{[math]}$ 下方 $\text{[math]}$ 上的一点，以点 $\text{[math]}$ ， $\text{[math]}$ 为顶点画一个直角三角形，使其第三个顶点也落在 $\text{[math]}$ 上，并使该直角三角形的一个内角与 $\text{[math]}$ 相等．
答案解析收藏纠错 + 选题
18. (2022九上·灌阳期中) 某商场销售一批衬衫，平均每天可销售出20件，每件盈利40元，为扩大销售盈利，商场决定采取适当的降价措施，但要求每件盈利不少于20元，经调查发现．若每件衬衫每降价1元，则商场每天可多销售2件．
1. （1）若每件衬衫降价4元，则每天可盈利多少元？
2. （2）若商场平均每天盈利1200元．则每件衬衫应降价多少元？
答案解析收藏纠错 + 选题
19. (2019九上·赣州期末) 在平面直角坐标系中，四边形ABCD的位置如图所示，请解答下列问题：
1. （1）将四边形ABCD先向左平移5个单位，再向下平移5个单位，得到四边形A₁B₁C₁D₁ ，画出平移后的四边形A₁B₁C₁D₁；
2. （2）将四边形A₁B₁C₁D₁绕点A₁逆时针旋转90°，得到四边形A₁B₂C₂D₂ ，画出旋转后的四边形A₁B₂C₂D₂ ，并写出点C₂的坐标．
3. （3）判断四边形A₁B₂C₂D₂是否可以看成由四边形ABCD绕着某点旋转一定角度所得，如果是，请直接写出这点的坐标；如果不是，请说明理由．
答案解析收藏纠错 + 选题
20. (2019九上·赣州期末) 如图，AB是⊙O的直径，延长弦BC到点D，使得CD＝BC，AD交⊙O于点E，连接BE．
1. （1）求证：AB＝AD；
2. （2）若AB＝8，∠DBE＝22.5°，求阴影部分的面积．
答案解析收藏纠错 + 选题
21. (2019九上·赣州期末) 创建文明城市，让老百姓住得更舒心，某社区决定把一块长50m，宽30m的矩形空地建成居民健身广场，设计方案如图，阴影部分为四个全等的矩形绿化区，剩余区域为活动区，且四周的出口宽度相同（其宽度不小于14m），设绿化区较长边为xm，活动区的面积为ym² ．
1. （1）请用含x的代数式表示矩形绿化区另一边长，并求出y与x的函数关系式（不要求写出自变量x的取值范围）；
2. （2）预计活动区造价为50元/m² ，绿化区造价为40元/m² ，若社区的此项建造投资费用不得超过72000元，求绿化区较长边x的取值范围．
答案解析收藏纠错 + 选题
22. (2019九上·赣州期末) 如图，在Rt△ABC中，∠ACB＝90°，以点B为圆心，BC长为半径画弧，交边AB与点D，连接CD．
1. （1）若∠A＝28°，求∠ACD的度数；
2. （2）若BC＝1，AC＝a．
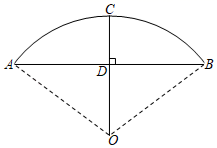
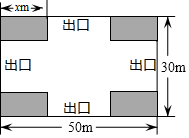
  ①直接写出线段AD的长为（用含字母a的式子表示）；
  
  ②判断线段AD的长是方程x²+2x﹣a²＝0的一个根吗？为什么？
答案解析收藏纠错 + 选题
23. (2019九上·赣州期末) 我们知道，二次函数y＝a（x﹣h）²+k（a≠0）的图象是一条抛物线，现定义一种变换，先作这条抛物线关于原点对称的抛物线y′，再将抛物线y′向上平移m（m＞0）个单位，得到新的抛物线y_m ，我们称y_m叫做二次函数y＝a（x﹣h）²+k（a≠0）的m阶变换．
1. （1）已知：二次函数y＝2（x+2）²+1，它的顶点关于原点的对称点为，这个抛物线的2阶变换的表达式为．
2. （2）若二次函数M的6阶变换的关系式为y₆＝（x﹣1）²+5．
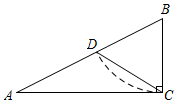
  ①二次函数M的函数表达式为．
  
  ②若二次函数M的顶点为点A，与x轴相交的两个交点中左侧交点为点B，动点P在抛物线y₆上，作PD⊥直线AB，请求出PD最小时P点的坐标．
答案解析收藏纠错 + 选题
24. (2019九上·赣州期末) 如图①，已知△ABC是等腰直角三角形，∠BAC＝90°，点D是BC的中点．作正方形DEFG，使点A，C分别在DG和DE上，连接AE，BG．
1. （1）试猜想线段BG和AE的数量关系，请直接写出你得到的结论；
2. （2）将正方形DEFG绕点D逆时针方向旋转一定角度后（旋转角度大于0°，小于或等于360°），如图②，通过观察或测量等方法判断（1）中的结论是否仍然成立？如果成立，请予以证明；如果不成立，请说明理由；
3. （3）若BC＝DE＝2，在（2）的旋转过程中，当AE为最大值时，求AF的值．
答案解析收藏纠错 + 选题