河南省商丘市柘城县2021年数学中考毕业会考试卷

更新时间：2021-11-29 浏览次数：178 类型：中考模拟

一、单选题

1. 在数轴上，点 $\text{[math]}$ 表示的数为 $\text{[math]}$ ，则下列各数在数轴上对应的点在点 $\text{[math]}$ 的左侧的是（）

A . -2 B . -1 C . 0 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021·青羊模拟) 被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST的反射面总面积相当于35个标准足球场的总面积.已知每个标准足球场的面积为 $\text{[math]}$ ，则FAST的反射面积总面积约为

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2016·扬州)
下列选项中，不是如图所示几何体的主视图、左视图、俯视图之一的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
4. 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. 如图，直线 $\text{[math]}$ ，等腰直角三角板 $\text{[math]}$ 的底角顶点 $\text{[math]}$ 落在 $\text{[math]}$ 上，直角顶点 $\text{[math]}$ 落在 $\text{[math]}$ 上，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . 70° B . 65° C . 60° D . 55°

答案解析收藏纠错 + 选题
6. 某校在八年级成立了书法、绘画、体育、歌舞手工五个兴趣小组，每位学生只能参加一个兴趣小组，学生会对学生参加情况进行了问卷调查，并初步绘制了扇形统计图（如图），但图中未显示歌舞和手工部分，请你根据图中信息判断参加歌舞兴趣小组的学生人数一定不可能是（）

A . 50人 B . 100人 C . 130人 D . 200人

答案解析收藏纠错 + 选题
7. 对于任意的实数 $\text{[math]}$ 和 $\text{[math]}$ ，定义一种运算 $\text{[math]}$ ，例如： $\text{[math]}$ .根据上述定义，不等式组 $\text{[math]}$ 的解集在数轴上表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2018·湖州) 某居委会组织两个检查组，分别对“垃圾分类”和“违规停车”的情况进行抽查．各组随机抽取辖区内某三个小区中的一个进行检查，则两个组恰好抽到同一个小区的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 如图，在平面直角坐标系中，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的坐标分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，再找一点 $\text{[math]}$ ，使它与点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 构成的四边形是平行四边形，则点 $\text{[math]}$ 的坐标不可能是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. 如图，以矩形 $\text{[math]}$ 的顶点 $\text{[math]}$ 为圆心，适当长为半径作弧，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ；再分别以点 $\text{[math]}$ ， $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的长为半径作弧，两弧交于点 $\text{[math]}$ ；作射线 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ .若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. 已知命题“对于正整数a，关于 x 的一元二次方程ax²-4x+1=0 没有实数根”，能说明这个命题是假命题的一个反例是a=.

答案解析收藏纠错 + 选题
13. (2011·河南) 已知点P（a，b）在反比例函数 $\text{[math]}$ 的图象上，若点P关于y轴对称的点在反比例函数 $\text{[math]}$ 的图象上，则k的值为．

答案解析收藏纠错 + 选题
14. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，以 $\text{[math]}$ 直径作圆， $\text{[math]}$ 为 $\text{[math]}$ 边的垂直平分线 $\text{[math]}$ 上一个动点，则图中阴影部分周长的最小值为.

答案解析收藏纠错 + 选题
15. 如图，正方形ABCD的边长是2，点E是CD边的中点，点F是边BC上不与点B，C重合的一个动点，把∠C沿直线EF折叠，使点C落在点C′处.当△ADC′为等腰三角形时，FC的长为.

答案解析收藏纠错 + 选题

三、解答题

16. 下面是同学进行分式化简求值的过程，请认真阅读并完成相应任务.
先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$

$\text{[math]}$

$\text{[math]}$ …第一步

$\text{[math]}$ …第二步

$\text{[math]}$ …第三步

$\text{[math]}$ …第四步

$\text{[math]}$ …第五步

$\text{[math]}$ …第六步

把 $\text{[math]}$ 代入上式得

原式 $\text{[math]}$

任务一：填空：①以上化简步骤中，第 ▲ 步是进行分式的通分，通分的依据是 ▲ ；

②第 ▲ 步开始出现错误，这一步错误原因是 ▲ ；

任务二：请直接写出该分式化简后的正确结果，然后再求值计算.

任务三：除纠正上述错误外，请你根据平时学习经验，就分式的化简求值时还需要注意的事项给其他同学提一条建议.

答案解析收藏纠错 + 选题
17. 2020年初，一场突如其来的疫情肆虐全国，为响应“停课不停学”的号召，某校采用“钉钉”和“腾讯会议”平台给学生授课，为了解这两个平台的实用性，学校组织全校学生对这两个平台进行打分（打分为整数，最低1分，最高5分），随机抽取20名学生的打分情况：
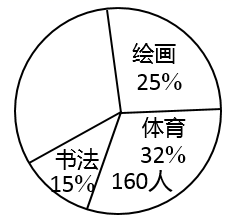
钉钉：5 4 5 1 4 2 5 3 4 1 1 3 5 4 2 4 4 3 2 5

腾讯会议：4 1 1 3 5 5 2 4 5 2 2 5 5 5 5 1 3 2 5 2

经整理，描述数据绘制了如下尚不完整的频数分布直方图和统计表.

平台

平均数

众数

中位数

钉钉

$\text{[math]}$

4

$\text{[math]}$

腾讯会议

3.35

$\text{[math]}$

$\text{[math]}$

分析数据、推断结论，请完成下列问题：
1. （1）请补全频数分布直方图；
2. （2）直接写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
3. （3）在求这20名学生给钉钉打分的平均数 $\text{[math]}$ 时，某同学是这样分析的：
  第一步：求平均数的公式是 $\text{[math]}$ ；
  
  第二步：此问题中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
  
  第三步： $\text{[math]}$ .
  
  ①某同学的分析是不正确的，他错在第几步?
  
  ②请你帮他计算出 $\text{[math]}$ 的值.
4. （4）你认为学生更喜欢的平台是（填“钉钉”或“腾讯会议”），理由是.
答案解析收藏纠错 + 选题
18. 阅读以下材料，并按要求完成相应的任务：
几何定论，是指变化的图形中某些几何元素的几何量保持不变（如定长、定角、定比、定积等），或几何元素间的某些性质或位置关系不变（如定点、定线、定方向等）如图①，点 $\text{[math]}$ 为 $\text{[math]}$ 外一点，过点 $\text{[math]}$ 为 $\text{[math]}$ 作直线与 $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为点 $\text{[math]}$ 关于 $\text{[math]}$ 的对称点，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，设 $\text{[math]}$ 的半径为 $\text{[math]}$ .

如图②，当过点 $\text{[math]}$ 的直线与 $\text{[math]}$ 相切时，点 $\text{[math]}$ ， $\text{[math]}$ 重合，可得 $\text{[math]}$ .

如图③，当过点 $\text{[math]}$ 的直线与 $\text{[math]}$ 相交时，证明 $\text{[math]}$ .

证明：如图③，连接OC、CD.

∵ $\text{[math]}$ 、 $\text{[math]}$ 关于 $\text{[math]}$ 对称，

∴ $\text{[math]}$ .

∴∠1＝∠2 .（依据）

…

任务：
1. （1）上述证明过程中的依据是；
2. （2）根据以上的证明提示，完成上述证明过程；
3. （3）如图③，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的半径.
答案解析收藏纠错 + 选题
19. (2020九上·东阿期中) 在“停课不停学”期间，小明用电脑在线上课，图1是他的电脑液晶显示器的侧面图，显示屏AB可以绕O点旋转一定角度．研究表明：当眼睛E与显示屏顶端A在同一水平线上，且望向显示器屏幕形成一个18°俯角（即望向屏幕中心P的的视线EP与水平线EA的夹角∠AEP）时，对保护眼睛比较好，而且显示屏顶端A与底座C的连线AC与水平线CD垂直时（如图2）时，观看屏幕最舒适，此时测得∠BCD＝30°，∠APE＝90°，液晶显示屏的宽AB为32cm．
1. （1）求眼睛E与显示屏顶端A的水平距离AE；（结果精确到1cm）
2. （2）求显示屏顶端A与底座C的距离AC．（结果精确到1cm）（参考数据：sin18°≈0.3，cos18°≈0.9，tan18°≈0.3， $\text{[math]}$ ≈1.4， $\text{[math]}$ ≈1.7）
答案解析收藏纠错 + 选题

20. 参照学习函数的过程方法，探究函数 $\text{[math]}$ 的图象与性质，因为 $\text{[math]}$ ，即 $\text{[math]}$ ，所以我们对比函数 $\text{[math]}$ 来探究列表：

$\text{[math]}$	…	-4	-3	-2	-1	$\text{[math]}$	$\text{[math]}$	1	2	3	4	…
$\text{[math]}$	…	$\text{[math]}$	$\text{[math]}$	1	2	4	-4	-2	-1	$\text{[math]}$	$\text{[math]}$	…
$\text{[math]}$	…	$\text{[math]}$	$\text{[math]}$	2	3	5	-3	-2	0	$\text{[math]}$	$\text{[math]}$	…

描点：在平面直角坐标系中以自变量 $\text{[math]}$ 的取值为横坐标，以 $\text{[math]}$ 相应的函数值为纵坐标，描出相应的点如图所示：

（1）请把 $\text{[math]}$ 轴左边各点和右边各点分别用一条光滑曲线，顺次连接起来；
（2）观察图象并分析表格，回答下列问题：
①当 $\text{[math]}$ 时， $\text{[math]}$ 随 $\text{[math]}$ 的增大而；（“增大”或“减小”）

② $\text{[math]}$ 的图象是由 $\text{[math]}$ 的图象向平移个单位而得到的；

③图象关于点中心对称.（填点的坐标）
（3）函数 $\text{[math]}$ 与直线 $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积.

答案解析收藏纠错 + 选题

21. 如图，在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ 和 $\text{[math]}$ .
1. （1）求抛物线的解析式；
2. （2）已知点 $\text{[math]}$ 与点 $\text{[math]}$ 关于此抛物线的对称轴对称，求点 $\text{[math]}$ 的坐标；
3. （3）点 $\text{[math]}$ 在抛物线上，且横坐标为4，记抛物线在点 $\text{[math]}$ ， $\text{[math]}$ 之间的部分（含点 $\text{[math]}$ ， $\text{[math]}$ ）为图象 $\text{[math]}$ ，若图象 $\text{[math]}$ 向下平移 $\text{[math]}$ $\text{[math]}$ 个单位后与直线 $\text{[math]}$ 只有一个公共点，求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
22. 问题情景：已知等腰直角三角形 $\text{[math]}$ 和等腰直角三角形 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点，连接 $\text{[math]}$ .
1. （1）大胆猜想：
  如图（1），当点 $\text{[math]}$ 在 $\text{[math]}$ 上，且点 $\text{[math]}$ 和点 $\text{[math]}$ 恰好重合时，探索 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系，并加以证明.
2. （2）尝试类比：
  如图（2），当点 $\text{[math]}$ 在 $\text{[math]}$ 上，点 $\text{[math]}$ 在 $\text{[math]}$ 外部时，（1）的结论还成立吗？若成立，请给予证明，若不成立，请说明理由.
3. （3）拓展延伸：
  如图（3），将图（2）中的等腰直角三角形 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ $\text{[math]}$ ，请猜想 $\text{[math]}$ 与 $\text{[math]}$ 之间的位置关系和数量关系.（不必证明）
答案解析收藏纠错 + 选题