山东省青岛市胶州市2021-2022学年九年级上学期期中数学...

更新时间：2022-01-07 浏览次数：83 类型：期中考试

一、单选题

1. (2022九上·雁塔月考) 下列各组中的四条线段成比例的是（）

A . 1，1，2，3 B . 1，2，3，4 C . 2，3，4，5 D . 2，3，6，9

答案解析收藏纠错 + 选题
2. (2023九上·连云月考) 下列式子是一元二次方程的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

3. (2021九上·胶州期中) “十一”长假期间，某玩具超市设立了一个如图所示的可以自由转动的转盘，开展有奖购买活动，顾客购买玩具就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应奖品．下表是该活动的一组统计数据：

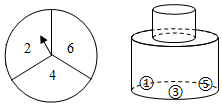
转动转盘的次数n	100	150	200	500	800	1000
落在“铅笔”区域的次数m	68	108	140	355	560	690
落在“铅笔”区域的频率 $\text{[math]}$	0.68	0.72	0.70	0.71	0.70	0.69

下列说法错误的是（）

A . 转动转盘20次，一定有6次获得“文具盒”铅笔文具盒 B . 转动转盘一次，获得“铅笔”的概率大约是0.70 C . 再转动转盘100次，指针落在“铅笔”区域的次数不一定是68次 D . 如果转动转盘3000次，指针落在“文具盒”区域的次数大约有900次

答案解析收藏纠错 + 选题

4. (2021九上·胶州期中) 如图，公路AC，BC互相垂直，公路AB的中点M与点C被湖隔开，若测得 $\text{[math]}$ km， $\text{[math]}$ km，则M，C两点之间的距离为（）

A . 10km B . 12km C . 13km D . 26km

答案解析收藏纠错 + 选题
5. (2021九上·胶州期中) 如图，在平行四边形ABCD中，EF//AB交AD于点E，交BD于点F， $\text{[math]}$ ， $\text{[math]}$ ，则CD的长为（）

A . 12 B . 7 C . 4 D . 3

答案解析收藏纠错 + 选题
6. (2024九下·涟水模拟) 定义运算： $\text{[math]}$ .例如 $\text{[math]}$ .则方程 $\text{[math]}$ 的根的情况为（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 无实数根 D . 只有一个实数根

答案解析收藏纠错 + 选题
7. (2021九上·胶州期中) 如图，点O为矩形ABCD的对称中心，点E从点A出发沿AB向点B运动，移动到点B停止，延长EO交CD于点F，则四边形AECF形状的变化依次为（）

A . 平行四边形→正方形→平行四边形→矩形 B . 平行四边形→菱形→平行四边形→矩形 C . 平行四边形→正方形→菱形→矩形 D . 平行四边形→菱形→正方形→矩形

答案解析收藏纠错 + 选题
8. (2021九上·胶州期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以其三边为边向外作正方形，延长EA交BG于点M，连接IM交BC于点N，若M是BG的中点，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2021九上·胶州期中) 在学校举办的“美德少年”评选活动中，九年级一班有甲，乙，丙，丁共4名学生获奖．班主任决定在这4名获奖学生中随机选出2名学生在班级进行主题演讲，则甲被选中的概率为．

答案解析收藏纠错 + 选题
10. (2021九上·胶州期中) 如图，C，D是线段AB的两个黄金分割点，且 $\text{[math]}$ ，则线段CD的长为米．

答案解析收藏纠错 + 选题
11. (2021九上·阳城期末) 某厂家2020年1~5月份的口罩产量统计如图所示，设从2月份到4月份，该厂家口罩产量的月平均增长率为 $\text{[math]}$ ，根据题意可得方程．

答案解析收藏纠错 + 选题
12. (2021九上·胶州期中) 如图，在△ABC中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则AC=．

答案解析收藏纠错 + 选题
13. (2021八下·乳山期中) 如图在菱形 $\text{[math]}$ 中， $\text{[math]}$ 是对角线 $\text{[math]}$ 上一动点过点 $\text{[math]}$ 作 $\text{[math]}$ 于 $\text{[math]}$ ． $\text{[math]}$ 于点 $\text{[math]}$ ．若菱形 $\text{[math]}$ 的周长为 $\text{[math]}$ ，面积为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
14. (2021九上·胶州期中) 如图，已知直线 $\text{[math]}$ ，过点 $\text{[math]}$ 作x轴的垂线交直线l于点 $\text{[math]}$ ，以 $\text{[math]}$ 为边作正方形 $\text{[math]}$ ，过点 $\text{[math]}$ 作x轴的垂线交直线l于点 $\text{[math]}$ ，以 $\text{[math]}$ 为边作正方形 $\text{[math]}$ ，…；则点 $\text{[math]}$ 的坐标为.

答案解析收藏纠错 + 选题

三、解答题

15. (2021九上·胶州期中) 已知如图，线段a．
求作：菱形ABCD，使该菱形边长和其中一条对角线长都为a．

答案解析收藏纠错 + 选题
16. (2021九上·胶州期中)
1. （1）用配方法解方程： $\text{[math]}$ ；
2. （2）若关于x的一元二次方程 $\text{[math]}$ 有一个解为 $\text{[math]}$ ，求k的值．
答案解析收藏纠错 + 选题
17. (2021九上·胶州期中) 如图，四边形ABCD的对角线互相平分，请你添加一个条件使之变为菱形，并说明理由．

答案解析收藏纠错 + 选题
18. (2021九上·胶州期中) 有一个可自由转动的转盘，被分成了三个大小相同的扇形，分别标有数字2，4，6；另有一个不透明的瓶子，装有分别标有数字1，3，5的三个完全相同的小球．小明先转动一次转盘，停止后记下指针指向的数字（若指针指在分界线上则重转），小刚再从瓶子中随机取出一个小球，记下小球上的数字．若得到的两数字之和是3的倍数，则小明赢；若得到的两数字之和是7的倍数，则小刚赢，你认为这个游戏公平吗？请说明理由．

答案解析收藏纠错 + 选题
19. (2021九上·胶州期中) 某小区在绿化工程中有一块长为 $\text{[math]}$ ，宽为 $\text{[math]}$ 的矩形空地，计划在其中修建两块相同的矩形绿地，使它们的面积之和为 $\text{[math]}$ ，两块绿地之间及周边留有宽度相等的人行通道（如图所示），求人行通道的宽度．

答案解析收藏纠错 + 选题
20. (2021九上·德惠期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，D为AC延长线上一点， $\text{[math]}$ ， $\text{[math]}$ ，过点D作DE//AB交BC的延长线于点E．
1. （1）求证： $\text{[math]}$ ；
2. （2）求DE的长度．
答案解析收藏纠错 + 选题
21. (2022九上·崂山期中) 已知：如图，在▱ABCD中，点E是BC的中点，连接AE并延长交DC的延长线于点F，连接BF．
1. （1）求证：△ABE≌△FCE；
2. （2）若AF＝AD，判断四边形ABFC的形状，并说明理由．
答案解析收藏纠错 + 选题
22. (2023九上·高台月考) 在“乡村振兴”行动中，某村办企业开发了一种成本价为50元/盒的有机产品，如果每盒的售价为60元时，每天可以销售200盒，通过市场调查发现，每盒售价每提高1元，每天少卖出10盒．该村办企业要想每天获得2240元利润，该有机产品的售价可以定为多少元/盒？

答案解析收藏纠错 + 选题
23. (2021九上·胶州期中) 问题提出：
将正m边形（ $\text{[math]}$ ）不断向外扩展，每扩展一个，正m边形每条边上的点的个数（以下简称“点数”）就增加一个，则n个正m边形的点数总共有多少个？

问题探究：

为了解决上面的问题，我们将采取一般问题特殊化的策略，先从简单和具体的情形入手：

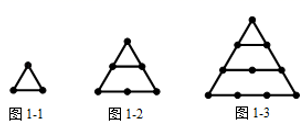
探究一：n个正三角形的点数总共有多少个？

如图1-1，1个正三角形的点数总共有 $\text{[math]}$ 个；

如图1-2，2个正三角形的点数总共有 $\text{[math]}$ 个；

如图1-3，3个正三角形的点数总共有 $\text{[math]}$ 个；

……

n个正三角形的点数总共有 $\text{[math]}$ 个．

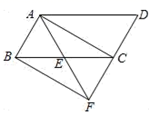
探究二：n个正四边形的点数总共有多少个？

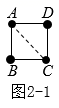
如图2-1，连接AC，得到两个三角形△ABC和△ADC，这两个三角形相同之处在于，BC边与CD边都有相同个数的点，即2个点．每个三角形都有3个点，两个三角形就是 $\text{[math]}$ 个点，因为这两个三角形在AC上有2个点重合，所以1个正四边形的点数总共有 $\text{[math]}$ （个）；

如图2-2，连接AC，得到两个三角形△ABC和△ADC，这两个三角形相同之处在于，BC边与CD边都有相同个数的点，即3个点，每个三角形都有6个点，两个三角形就是 $\text{[math]}$ 个点，因为这两个三角形在AC上有3个点重合，所以2个正四边形的点数总共有 $\text{[math]}$ （个）；

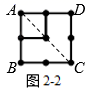
如图2-3，连接AC，得到两个三角形△ABC和△ADC，这两个三角形相同之处在于，BC边与CD边都有相同个数的点，即4个点．每个三角形都有10个点，两个三角形就是 $\text{[math]}$ 个点，因为这两个三角形在AC上有4个点重合，所以3个正四边形的点数总共有 $\text{[math]}$ （个）；

……

n个正四边形的点数总共有 $\text{[math]}$ $\text{[math]}$ ，即 $\text{[math]}$ 个．

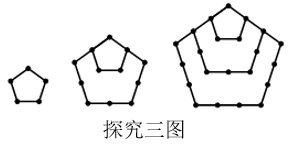
探究三：n个正五边形的点数总共有多少个？

类比探究二的方法：

1个正五边形的点数总共有5个；

2个正五边形的点数总共有12个；

3个正五边形的点数总共有个；

……

n个正五边形的点数总共有个．

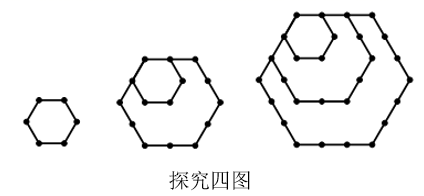
探究四：n个正六边形的点数总共有个．

问题解决：

n个正m边形的点数总共有个．

实际应用：

若9个正m边形的点数总共有820个，则m的值为．

答案解析收藏纠错 + 选题
24. (2021九上·胶州期中) 如图，四边形ABCD中，AD//BC， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点M从点D出发，以每秒2个单位长度的速度向点A运动，同时，点N从点B出发，以每秒1个单位长度的速度向点C运动．当其中一个动点到达终点时，另一个动点也随之停止运动．过点N作 $\text{[math]}$ 于点P，连接AC交NP于点Q，连接MQ，设运动时间为t秒（ $\text{[math]}$ ）
1. （1）连接AN，CP，当t为何值时，四边形ANCP为平行四边形；
2. （2）设四边形DMQC的面积为y，求y与t的函数关系式；
3. （3）在运动过程中，是否存在某一时刻t，使四边形DMQC的面积与△ABC的面积相等？若存在，求出t的值；若不存在，请说明理由；
4. （4）将△AQM沿AD翻折，得到△AKM．在运动过程中，是否存在某时刻t，使四边形AQMK为菱形，若存在，求出t的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题