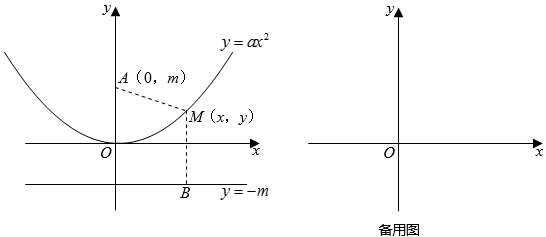
B .
B .  D .
D . 
 B .
B .  C .
C .  D .
D . 




⑴作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1(只画出图形)
⑵作出△ABC关于原点O成中对心称的△A2B2C2 , (只画出图形),写出B2和C2的坐标.
⑶请在轴上找一点P,使PB1+PC1的值最小,并直接写出点P的坐标.



①如图2,在正方形OABC旋转过程中,线段AM,MN,NC之间满足什么样的数量关系?请说明理由;
②当ACMN时,求S△BMN .