吉林省长春市长春净月高新技术产业开发区2021-2022学年...

更新时间：2022-03-01 浏览次数：91 类型：期末考试

一、单选题

1. (2023七上·深圳期中) 2022的相反数是（）

A . 2022 B . -2022 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023七上·利州期末) 2021年12月9日，“天宫课堂”第一课在中国空间站正式开讲．遍布各个测控站点的统一测控系统与架设在太空36000千米的中继卫星组网运行，提供天地之间的图象传输．请将36000用科学记数法表示为（）

A . 3.6×10⁵ B . 36×10³ C . 3.6×10⁴ D . 3.6×10³

答案解析收藏纠错 + 选题
3. (2022七上·历城期末) 一个由5个相同的正方体组成的立体图形，如图所示，则这个立体图形的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2021七上·净月期末) 已知代数式﹣5xyⁿ与3x^my³是同类项，则m，n的值分别为（）

A . 0，3 B . 1，3 C . 3，0 D . 3，1

答案解析收藏纠错 + 选题
5. (2021七上·红桥期末) 实数a、b、c、d在数轴上的对应点的位置如图所示，在这四个数中，绝对值最小的数是（）

A . a B . b C . c D . d

答案解析收藏纠错 + 选题
6. (2021七上·净月期末) 如图， $\text{[math]}$ 是北偏东30°方向的一条射线，若射线 $\text{[math]}$ 与射线 $\text{[math]}$ 垂直．则 $\text{[math]}$ 的方向角是（）

A . 北偏西30° B . 北偏西60° C . 东偏北30° D . 东偏北60°

答案解析收藏纠错 + 选题
7. (2021七上·净月期末) 如图，若要使 $\text{[math]}$ 与 $\text{[math]}$ 平行，则 $\text{[math]}$ 绕点 $\text{[math]}$ 至少旋转的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021七上·净月期末) 如图，点A是直线l外一点，过点A作AB⊥l于点B．在直线l上取一点C，连结AC，使AC＝ $\text{[math]}$ AB，点P在线段BC上，连结AP．若AB＝3，则线段AP的长不可能是（）

A . 3.5 B . 4 C . 5 D . 5.5

答案解析收藏纠错 + 选题

二、填空题

9. (2023七上·浈江期中) 比较大小：﹣2 ﹣3．

答案解析收藏纠错 + 选题
10. (2021七上·净月期末) 将多项式3x²y﹣6y²+x³﹣x按x降幂排列为．

答案解析收藏纠错 + 选题
11. (2021七上·净月期末) 若a＞0，b＜0，|a|＞|b|，则a+b0（用“＞”或“＜”填空）．

答案解析收藏纠错 + 选题
12. (2021七上·净月期末) 代数式x²+x+3的值为7，则代数式2x²+2x﹣3的值为．

答案解析收藏纠错 + 选题
13. (2021七上·净月期末) 如图，EF、EG分别是∠AEB和∠BEC的平分线．若∠BEF＝30°，则∠BEG＝°．

答案解析收藏纠错 + 选题
14. (2022七上·淅川期中) 如图是一组有规律的图案，它们是由边长相等的正三角形组合而成，第 $\text{[math]}$ 个图案有 $\text{[math]}$ 个三角形，第 $\text{[math]}$ 个图案有 $\text{[math]}$ 个三角形，第 $\text{[math]}$ 个图案有 $\text{[math]}$ 个三角形 $\text{[math]}$ 按此规律摆下去，第 $\text{[math]}$ 个图案有个三角形（用含 $\text{[math]}$ 的代数式表示）．

答案解析收藏纠错 + 选题

三、解答题

15. (2021七上·净月期末) 计算：
1. （1）（﹣6）+5+（﹣2）；
2. （2）（﹣4）×（﹣3）×（﹣25）；
3. （3） $\text{[math]}$ ；
4. （4） 2×（﹣3）²﹣4÷（﹣2）﹣10．
答案解析收藏纠错 + 选题
16. (2021七上·净月期末) 先化简，再求值：（3x²﹣xy+2y²）﹣2（x²﹣ $\text{[math]}$ xy+y²），其中x＝﹣2，y＝ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2023七上·滦州期中) 如图，已知线段AB＝24cm，延长AB至C，使得BC＝ $\text{[math]}$ AB，
1. （1）求AC的长；
2. （2）若D是AB的中点，E是AC的中点，求DE的长．
答案解析收藏纠错 + 选题
18. (2021七上·净月期末) “新冠肺炎”疫情的蔓延，使得医用口罩销量大幅增加，某口罩加工厂为满足市场需求计划每天生产5000个，实际每天生产量与计划相比有出入，把某一周的生产情况记录如下（超产为正，减产为负，单位：个）：
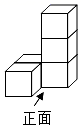
星期
一
二
三
四
五
六
日
增减
+100
﹣150
+350
﹣200
+300
﹣100
+150
1. （1）产量最多的一天比产量最少的一天多生产多少个？
2. （2）该工厂本周一共生产多少个口罩？
答案解析收藏纠错 + 选题
19. (2021七上·净月期末) 如图，已知直线l和直线外三点A、B、C，按下列要求画图：
（ 1 ）画射线AB；
（ 2 ）画线段BC；
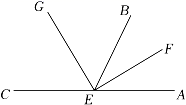
（ 3 ）点E在直线l上移动，要使AE+CE最小，请先确定点E的位置，并说明你的依据是 ▲ ．

答案解析收藏纠错 + 选题
20. (2021七上·净月期末) 如图，数轴上点B表示的数为2，点B在数轴上向左移动12个单位长度到达点A，点B在数轴上向右移动4个单位长度到达点C．
1. （1）点A表示的数是，点C表示的数是．
2. （2）动点P、Q同时分别从A，C出发，点P以每秒4个单位长度的速度沿数轴向右匀速运动，点Q以每秒2个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．则点P表示的数是，点Q表示的数是．（用含t的代数式表示）
答案解析收藏纠错 + 选题
21. (2021七上·净月期末) 如图，已知AE $\text{[math]}$ BF，AC⊥AE，BD⊥BF，AC与BD平行吗？补全下面的解答过程（理由或数学式）．
解：∵AE $\text{[math]}$ BF，
∴∠EAB＝                  ▲                   ．（                  ▲                  ）
∵AC⊥AE，BD⊥BF，
∴∠EAC＝90°，∠FBD＝90°．
∴∠EAC＝∠FBD（                  ▲                  ）
∴∠EAB﹣                  ▲                  ＝∠FBG﹣                  ▲                   ，
即∠1＝∠2．
∴                  ▲                   $\text{[math]}$                   ▲                  （                  ▲                  ）．

答案解析收藏纠错 + 选题
22. (2021七上·净月期末)
1. （1）如图1，将一副直角三角尺的直角顶点C叠放在一起，经探究发现∠ACB与∠DCE的和不变．证明过程如下：
  由题可知∠BCE＝∠ACD＝90°
  ∴∠ACB＝ +∠BCD．
  ∴∠ACB＝90°+∠BCD．
  ∴∠ACB+∠DCE
  ＝90°+∠BCD+∠DCE
  ＝90°+∠BCE
  ∵∠BCE＝90°，
  ∴∠ACB+∠DCE＝．
2. （2）如图2，若将两个含有60°的三角尺叠放在一起，使60°锐角的顶点A重合，则∠DAB与∠CAE有怎样的数量关系，并说明理由；
3. （3）如图3，已知∠AOB＝α，∠COD＝β（α，β都是锐角），若把它们的顶点O重合在一起，请直接写出∠AOD与∠BOC的数量关系．
答案解析收藏纠错 + 选题
23. (2021七上·净月期末) 七年级地理教材第三章《天气与气候》中讲解了“气温的垂直变化”；在山地和丘陵，气温随海拔升高而降低．大致每升高100米，气温约下降0.6℃．一名同学在山脚下测得此处的海拔是720米，气温是28.8℃．
1. （1）若山顶的海拔是1520米，则海拔升高多少米？气温应该是多少？
2. （2）若山上某处的海拔是x米，请用含x的代数式表示此处的气温为℃．
3. （3）张老师爬到山上某处看了一下随身携带的温度计，气温为27℃，你能求出此处的海拔吗？请说明理由．
答案解析收藏纠错 + 选题
24. (2021七上·净月期末) 已知AM $\text{[math]}$ CN，点B在直线AM、CN之间，AB⊥BC于点B．
1. （1）如图1，请直接写出∠A和∠C之间的数量关系：．
2. （2）如图2，∠A和∠C满足怎样的数量关系？请说明理由．
3. （3）如图3，AE平分∠MAB，CH平分∠NCB，AE与CH交于点G，则∠AGH的度数为．
答案解析收藏纠错 + 选题