2021年内蒙古鄂尔多斯东胜区中考二模数学试卷

更新时间：2022-03-28 浏览次数：54 类型：中考模拟

一、单选题

1. (2021·东胜模拟) 在数轴上表示与2的点距离2个单位长度的数是（）

A . 0 B . 4 C . 0或4 D . 2

答案解析收藏纠错 + 选题
2. (2021·东胜模拟) 如图是某种几何体的实物图，则与该几何体相对应的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022·双辽模拟) 截止2021年4月17日，全国接种新冠病毒疫苗达到 $\text{[math]}$ 剂次，则数据 $\text{[math]}$ 表示的原数是（）

A . 1898000 B . 18980000 C . 189800000 D . 1898000000

答案解析收藏纠错 + 选题
4. (2021·东胜模拟) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021·东胜模拟) 在“博爱一日捐”活动中，某校初二级部50名教师参与献爱心，以下是捐款统计表：
金额/元
50
100
150
200
300
人数
4
18
14
8
6
则该校初二教师捐款金额的中位数、众数分别是（）

A . 100，100 B . 100，150 C . 150，100 D . 150，150

答案解析收藏纠错 + 选题
6. (2021·东胜模拟) 如图，已知钝角 $\text{[math]}$ 中， $\text{[math]}$ 且 $\text{[math]}$ ，（1）以C为圆心， $\text{[math]}$ 长为半径画弧；（2）以B为圆心， $\text{[math]}$ 为半径画弧，交前弧于点E；（3）连接AE交 $\text{[math]}$ 的延长线于点D．下列叙述不一定正确的是（）

A . $\text{[math]}$ 是等边三角形 B . $\text{[math]}$ 平分 $\text{[math]}$ C . $\text{[math]}$ D . BD垂直平分AE

答案解析收藏纠错 + 选题
7. (2022·鄂伦春模拟) 随着市场对新冠疫苗需求越来越大，为满足市场需求，某大型疫苗生产企业更新技术后，加快了生产速度，现在平均每天比更新技术前多生产10万份疫苗，现在生产500万份疫苗所需的时间与更新技术前生产400万份疫苗所需时间少用5天，设现在每天生产x万份，据题意可列方程（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021九上·宁波期中) 如图，四边形 $\text{[math]}$ 是半径为2的 $\text{[math]}$ 的内接四边形，连接 $\text{[math]}$ .若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021·东胜模拟) 现有下列命题：①对角线相等且互相平分的四边形是矩形；②有两条边长比值是3：4的两个直角三角形相似：③若一元二次方程 $\text{[math]}$ 有实数根，则 $\text{[math]}$ ；④若点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，且 $\text{[math]}$ ，则a的取值范围是 $\text{[math]}$ ．其中是真命题的是（）

A . ①② B . ②③ C . ③④ D . ①④

答案解析收藏纠错 + 选题
10. (2021·东胜模拟) 如图1，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ；动点P以每秒1个单位的速度从点A出发沿线段 $\text{[math]}$ 运动到点B，同时动点Q以每秒4个单位的速度从点B出发，沿折线 $\text{[math]}$ 运动到点D．图2是点P、Q运动时， $\text{[math]}$ 的面积S随运动时间t变化关系的图象，则a的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. 函数y= $\text{[math]}$ 中自变量x的取值范围是．

答案解析收藏纠错 + 选题
12. (2021·东胜模拟) 如图，小明自制一块乒乓球拍，正面是半径为 $\text{[math]}$ 的 $\text{[math]}$ ， $\text{[math]}$ 的长为 $\text{[math]}$ ，弓形 $\text{[math]}$ （阴影部分）粘贴胶皮，则胶皮面积为．

答案解析收藏纠错 + 选题
13. (2021·东胜模拟) 如图，O是坐标原点，菱形 $\text{[math]}$ 的顶点A的坐标为 $\text{[math]}$ ，顶点C在x轴的正半轴上，函数 $\text{[math]}$ 的图象经过顶点B，则k的值为．

答案解析收藏纠错 + 选题
14. (2021·东胜模拟) 如图，点A、B、C是圆O上的三点，且四边形ABCO是平行四边形，OF⊥OC交圆O于点F，则∠BAF=．

答案解析收藏纠错 + 选题
15. (2021·东胜模拟) 如图，在平面直角坐标系中， $\text{[math]}$ 将 $\text{[math]}$ 绕A顺时针旋转得到 $\text{[math]}$ ，此时 $\text{[math]}$ ﹔将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转得到 $\text{[math]}$ ，此时 $\text{[math]}$ 将 $\text{[math]}$ 绕点 $\text{[math]}$ 继续顺时针旋转，此时 $\text{[math]}$ …按此规律继续旋转，直至得到点 $\text{[math]}$ 为止，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2021·东胜模拟) 如图，在平面直角坐标系中，O为坐标原点， $\text{[math]}$ ，点B在y轴上运动，以 $\text{[math]}$ 为边作等腰 $\text{[math]}$ ， $\text{[math]}$ （点A，B，C按照顺时针排列），当点B在y轴上运动时，点C也随之运动．在点C的运动过程中， $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题

三、解答题

17. (2021·东胜模拟)
1. （1）解不等式组 $\text{[math]}$ ，并求出其整数解．
2. （2）先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2021·东胜模拟) 某中学开展了“师生共读”，营造"书香校园"的读书活动．为了了解学生在此次活动中的读书情况，现随机抽取部分学生进行调查，将收集到的数据整理，并绘制成如图所示不完整的折线统计图和扇形统计图．
1. （1）本次调查共随机抽取名学生，阅读量为2本学生所在扇形的圆心角度数是度，并补全折线统计图；
2. （2）根据调查情况，现决定在读书数量为1本和4本的学生中任选两名学生进行交流，请用树状图或列表法求这两名学生读书数量均为1本的概率．
答案解析收藏纠错 + 选题
19. (2021·东胜模拟) A、B两地相距400千米，某人开车从A地匀速到B地，设小汽车的行驶时间为t小时，行驶速度为v千米/小时，且全程限速，速度不超过100千米/小时．
1. （1）写出v关于t的函数表达式；
2. （2）若某人开车的速度不超过每小时80千米，那么他从A地匀速行驶到B地至少要多长时间？
3. （3）若某人上午7点开车从A地出发，他能否在10点40分之前到达B地？请说明理由．
答案解析收藏纠错 + 选题
20. (2021·东胜模拟) 阅读以下文字并解答问题：在“测量物体的高度”活动中，某数学兴趣小组的3名同学选择了测量学校里的三棵树的高度，在同一时刻的阳光下，他们分别做了以下工作：
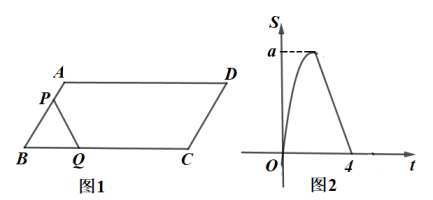
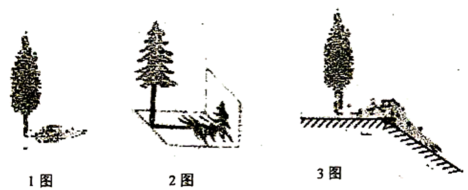
小芳：测得一根长为1米的竹竿的影长为0.8米，甲树的影长为4.08米（如1图）．
小华：发现乙树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上（如2图），墙壁上的影长为1.2米，落在地面上的影长为2.4米．
小明：测得丙树落在地面上的影长为2.4米，落在坡面上影长为3.2米（如3图）．身高是1.6米的小明站在坡面上，影子也都落坡面上，小芳测得他的影长为2米．
1. （1）在横线上直接填写甲树的高度为米，乙树的高度为米﹔
2. （2）请求出丙树的高度．
答案解析收藏纠错 + 选题
21. (2021·东胜模拟) 如图，点D、E在以AB为直径的 $\text{[math]}$ 上，AE与 $\text{[math]}$ 交于点F， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若点E是 $\text{[math]}$ 的中点， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
22. (2021·东胜模拟) 某商店销售一种商品，经市场调查发现：该商品的周销售量y（件）是售价x（元/件）的一次函数，其售价、周销售量、周销售利润w（元）的三组对应值如表：
售价x（元/件）
60
70
80
周销售量y（件）
100
80
60
周销售利润w（元）
2000
2400
2400
注：周销售利润＝周销售量×（售价﹣进价）
1. （1） ①求y关于x的函数解析式．（不要求写出自变量的取值范围）
  ②该商品进价是 ▲ 元/件；当售价是 ▲ 元/件时，周销售利润最大，最大利润是 ▲ 元．
2. （2）由于某种原因，该商品进价提高了m元/件（m＞0），物价部门规定该商品售价不得超过70元/件，该商店在今后的销售中，周销售量与售价仍然满足（1）中的函数关系．若周销售最大利润是1600元，求m的值．
答案解析收藏纠错 + 选题
23. (2021·东胜模拟) 如图，已知直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 相交于A，B两点，抛物线的顶点是 $\text{[math]}$ ，点B在x轴上．
1. （1）求抛物线的解析式；
2. （2）若点M是y轴上一点，点N是坐标平面内一点，当以A、B、M、N为顶点的四边形是矩形时，求点M的坐标．
3. （3）在抛物线上是否存在点Q，使 $\text{[math]}$ ，若存在，请直接写出点Q的横坐标；若不存在，说明理由．
答案解析收藏纠错 + 选题
24. (2021·东胜模拟)
1. （1）【问题发现】
  若四边形 $\text{[math]}$ 是菱形， $\text{[math]}$ ，点P是射线BD上一动点，以 $\text{[math]}$ 为边向右侧作等边 $\text{[math]}$ ，如图1，当点E在菱形 $\text{[math]}$ 内部或边上时，连接 $\text{[math]}$ ，则BP与 $\text{[math]}$ 有怎样的数量关系？并说明理由；
2. （2）【类比探究】
  若四边形 $\text{[math]}$ 是正方形，点P是射线BD上一动点，以 $\text{[math]}$ 为直角边在 $\text{[math]}$ 边的右侧作等腰 $\text{[math]}$ ，其中 $\text{[math]}$ ，如图2.当点P在对角线BD上，点E恰好在 $\text{[math]}$ 边所在直线上时，则BP与 $\text{[math]}$ 之间的数量关系？并说明理由；
3. （3）【拓展延伸】
  在（2）的条件下，如图3，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ，当P是对角线BD的延长线上一动点时，连接BE，若 $\text{[math]}$ ，求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题