湖北省襄阳市2021年中考数学模拟试卷

更新时间：2022-04-28 浏览次数：90 类型：中考模拟

一、单选题

1. 下列各数中是无理数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 在下列四个实数中，最大的数是（）

A . ﹣1 B . ﹣ $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2019八上·长沙月考) 如图，在△ABC中，∠B＝55°，∠C＝63°，DE∥AB，则∠DEC等于（）

A . 63° B . 62° C . 55° D . 118°

答案解析收藏纠错 + 选题
4. 下列图形中，只有两条对称轴的是（）

A . 正六边形 B . 矩形 C . 等腰梯形 D . 圆

答案解析收藏纠错 + 选题
5. 不等式组 $\text{[math]}$ 的解表示在数轴上，正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. 下列说法正确的是（）

A . 平行四边形既是中心对称图形也是轴对称图形 B . 矩形的对角线不可能垂直 C . 菱形的对角线不可能相等 D . 对角线互相平分、垂直且相等的四边形是正方形

答案解析收藏纠错 + 选题
7. 已知一组数据为5，7， $\text{[math]}$ ， 3，4，6，若这组数据的平均数为5，则这组数据的方差为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 10

答案解析收藏纠错 + 选题
8. (2020八上·凤县期末) 我国古代数学名著《孙子算经》记载一道题，大意为100个和尚吃了100个馒头，已知1个大和尚吃3个馒头，3个小和尚吃1个馒头，问有几个大和尚，几个小和尚？若设有 $\text{[math]}$ 个大和尚， $\text{[math]}$ 个小和尚，那么可列方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的弦， $\text{[math]}$ ， $\text{[math]}$ 的延长线交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 长为（）

A . 3 B . 4 C . 5 D . 8

答案解析收藏纠错 + 选题
10. 二次函数 $\text{[math]}$ 的图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

11. (2020八上·科尔沁期末) 数0.0000046用科学记数法表示为：．

答案解析收藏纠错 + 选题
12. (2017八下·江都期中) 若分式 $\text{[math]}$ 的值为0，则x的值为．

答案解析收藏纠错 + 选题
13. 在一个不透明的口袋中装有4个完全相同的小球，把它们分别标号为1，2，3，4，从中随机摸出两个小球，其标号之和大于4的概率为.

答案解析收藏纠错 + 选题
14. 飞机着陆后滑行的距离s（单位：m）关于滑行的时间t（单位：s）的函数解析式是s＝60t﹣1.5t² ，飞机着陆后滑行米才能停下来.

答案解析收藏纠错 + 选题
15. 如图，在直线l上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别为1.0，1.21，1.44，正放置的四个正方形的面积为S₁、S₂、S₃、S₄ ，则S₁+S₂+S₃+S₄=.

答案解析收藏纠错 + 选题
16. (2017八上·雅安期末) 边长为2 $\text{[math]}$ 的正方形的对角线长为．

答案解析收藏纠错 + 选题

三、解答题

17. (2019八上·济宁期中) 先化简，再从﹣1、2、3、4中选一个合适的数作为x的值代入求值． $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. 如图，在△ABC中，AB=AC，∠BAC=120°，AB边上的垂直平分线与AB、BC交于点D、E，AC边上的垂直平分线与AC、BC分别交于点G、F，
1. （1） △AEF是什么形状？你能证明吗？
2. （2）连结DG，你能根据学过的相似三角形的知识证明DG= $\text{[math]}$ BC吗？
3. （3） DG=5cm，试求△AEF的周长.
答案解析收藏纠错 + 选题
19. (2016·丹东)
为了促进学生多样化发展，某校组织开展了社团活动，分别设置了体育类、艺术类、文学类及其它类社团（要求人人参与社团，每人只能选择一项）．为了解学生喜爱哪种社团活动，学校做了一次抽样调查．根据收集到的数据，绘制成如下两幅不完整的统计图，请根据图中提供的信息，完成下列问题：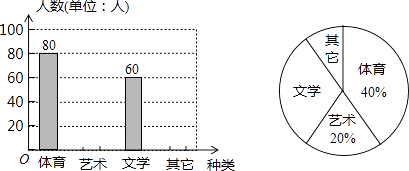
1. （1）此次共调查了多少人？
2. （2）求文学社团在扇形统计图中所占圆心角的度数；
3. （3）请将条形统计图补充完整；
4. （4）若该校有1500名学生，请估计喜欢体育类社团的学生有多少人？
答案解析收藏纠错 + 选题
20. 如图所示，某中学九年级数学活动小组选定测量学校前面小河对岸大树 $\text{[math]}$ 的高度，他们在斜坡上 $\text{[math]}$ 处测得大树顶端 $\text{[math]}$ 的仰角是 $\text{[math]}$ ，朝大树方向下坡走6米到达坡底 $\text{[math]}$ 处，在 $\text{[math]}$ 处测得大树顶端 $\text{[math]}$ 的仰角是 $\text{[math]}$ ，若斜坡 $\text{[math]}$ 的坡比 $\text{[math]}$ ： $\text{[math]}$ ，求大树的高度.（结果保留整数）参考数据：（ $\text{[math]}$ 取1.7）

答案解析收藏纠错 + 选题

21. (2020九下·北碚月考) 已知关于x函数y＝|﹣x²+bx﹣7|﹣4，点（4，5）在函数上，且b为整数，根据我们已有的研究函数的经验，请对该函数及其图象进行如下探究，并完成以下问题：

（1）求b＝；

（2）函数图象探究：

①下表是y与x的几组对应值，请直接写出m与n的值：m＝▲ ， n＝▲；

x	…	﹣ $\text{[math]}$	0	$\text{[math]}$	1	2	3	4	5	6	7	7 $\text{[math]}$	8	8 $\text{[math]}$	…
y	…	m	3	$\text{[math]}$	﹣4	1	4	n	4	1	﹣4	$\text{[math]}$	3	5 $\text{[math]}$	…

②根据你喜欢的方式，在如图所示的平面直角坐标系中，画出该函数图象；

（3）结果函数图象，写出该函数的一条性质：；
（4）若关于x的方程|﹣x²+bx﹣7|＝m+4有四个根，则m的取值范围为.

答案解析收藏纠错 + 选题

22. 如图，线段 $\text{[math]}$ ，以线段 $\text{[math]}$ 为直径画 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 上的动点，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的切线与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）点 $\text{[math]}$ 在线段 $\text{[math]}$ 的哪个位置时，四边形 $\text{[math]}$ 为正方形？请说明理由.
答案解析收藏纠错 + 选题
23. (2020八下·冠县期末) 某销售商计划购进甲、乙两种商品共 $\text{[math]}$ 件进行销售.已知甲种商品每件进价 $\text{[math]}$ 元，乙种商品每件进价 $\text{[math]}$ 元；通过市场考察，销售商决定甲种商品以每件 $\text{[math]}$ 元的价格出售，乙种商品以每件 $\text{[math]}$ 元的价格出售.设销售商购进的甲种商品有x件，销售完甲、乙两种商品后获得的总利润为y元
1. （1）求y与x的函数关系式；
2. （2）如果销售商购进的甲种商品的数量不少于乙种商品数量的 $\text{[math]}$ 倍，请求出获利最大的进货方案，所获得的最大利润是多少元？
答案解析收藏纠错 + 选题
24. 在直角坐标系中，已知点 $\text{[math]}$ 、 $\text{[math]}$ 的坐标是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 满足方程组 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 轴正半轴上一点，且 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点的坐标；
2. （2）是否存在点 $\text{[math]}$ ，使 $\text{[math]}$ ？若存在，请求出 $\text{[math]}$ 点坐标；若不存在，请说明理由；
3. （3）若点 $\text{[math]}$ 沿 $\text{[math]}$ 轴负半轴方向以每秒1个单位长度平移至点 $\text{[math]}$ ，当运动时间 $\text{[math]}$ 为多少秒时，四边形 $\text{[math]}$ 的面积 $\text{[math]}$ 为15个平方单位？求出此时点 $\text{[math]}$ 的坐标.
4. （4）连接 $\text{[math]}$ 、 $\text{[math]}$ ，若 $\text{[math]}$ 为 $\text{[math]}$ 上一动点（不与 $\text{[math]}$ 、 $\text{[math]}$ 重合）连接 $\text{[math]}$ 、 $\text{[math]}$ ，探究点 $\text{[math]}$ 在运动过程中， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系并证明.
答案解析收藏纠错 + 选题
25. (2019·长春模拟) （问题提出）
如图①，在 $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 边上的中线 $\text{[math]}$ 的取值范围.
1. （1）【问题解决】
  解决此问题可以用如下方法：延长 $\text{[math]}$ 到点 $\text{[math]}$ 使 $\text{[math]}$ ，再连接 $\text{[math]}$ （或将 $\text{[math]}$ 绕着点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ），把 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 集中在 $\text{[math]}$ 中，利用三角形三边的关系即可判断，由此得出中线 $\text{[math]}$ 的取值范围.
2. （2）【应用】
  如图②，在 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 的中点，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
3. （3）【拓展】
  如图③，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是边 $\text{[math]}$ 的中点，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，过点 $\text{[math]}$ 作 $\text{[math]}$ 交边 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ 。已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题