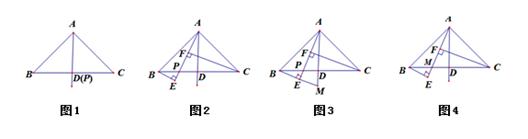
进球数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
场数 | 1 | 15 | 19 | 18 | 4 | 2 | 2 | 3 |

①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.
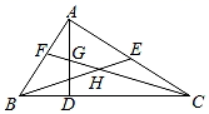
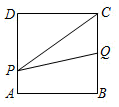
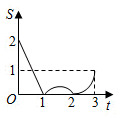 B .
B .  C .
C . 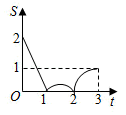 D .
D . 

⑴把向右平移5个单位后得到
B
C
, 请画出
B
C
, 并写出
的坐标;
⑵把绕点C逆时针旋转90°,得到
B
C
, 请画出
B
C
, 并写出
的坐标.
(≈1.73).



分组 | 频数 | 频率 |
第一组(0≤x<15) | 3 | 0.15 |
第二组(15<x <30 ) | 6 | a |
第三组(30<x<45) | 7 | 0.35 |
第四组(45≤x <60) | b | 0.20 |



求这个二次函数的表达式;