2022年北师大数学七下期中复习阶梯训练：整式的乘除（优生加...

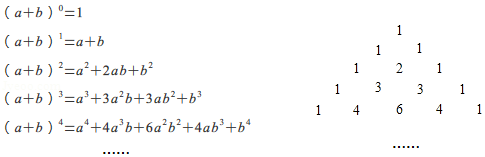
然后在①式的两边都乘以6，得： ……②

②-①得 ，即 ，所以 .

得出答案后，爱动脑筋的小林想：如果把“6”换成字母“a”(a≠0且a≠1)，能否求出 的值?你的答案是（   ）

例如： ，它只有一项，系数为1；系数和为1；

，它有两项，系数分别为1，1，系数和为2；

，它有三项，系数分别为1，2，1，系数和为4；

，它有四项，系数分别为1，3，3，1，系数和为8； ，

则 的展开式共有项，系数和为.

（x﹣1）（x+1）＝x²﹣1；

（x﹣1）（x²+x+1）＝x³﹣1；

（x﹣1）（x³+x²+x+1）＝x⁴﹣1；

…

请你根据以上等式的规律，完成下列问题：

⑴（x﹣1）（xⁿ+…+x²+x+1）＝﹣1；

⑵计算：1+2+2²+…+2²⁰¹⁹＝．

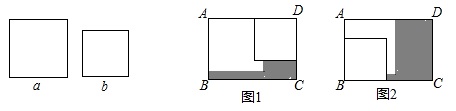
①图2中的阴影部分的面积为；

②观察图2请你写出（a+b）²、（a﹣b）²、ab之间的等量关系是；

③根据（2）中的结论，若x+y=5，x•y= ，则（x﹣y）²=；

④实际上通过计算图形的面积可以探求相应的等式．

如图3，你发现的等式是．

小张介绍了他的计算奥秘：将最后的得数减去200，所得的结果百位数就是第一个数，十位数就是第二个数，个位数就是第三个数．

探究一：证明小张想法的符合题意性

小张将最后的得数减去200：

，

所以结果百位数就是第一个数，十位数就是第二个数，个位数就是第三个数．小李听完后深受启发也设计了自己的运算程序，让小张随便选三个一位数按这样的步骤去运算：

①把第一个数乘5，再加上5；

②把第二个数乘20，再加上2；

③将①的运算结果与②的运算结果相乘，再加上第三个数；

④减去第一个数与第二个数乘积的100倍．

小李说：“只要小张告诉我最后的得数，我就能知道小张一开始所想的三个一位数。”

小李是如何知道的呢？请你模仿探究一的证明过程填写下表：

探究二：证明小李想法的符合题意性

请介绍小李的计算奥秘，描述：你是怎样由最后的得数，识别出最初选定的三个一位数的？

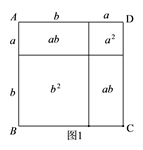
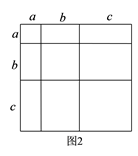
① 类比教材中的方法，由图2中的大正方形可得等式：                          .

② 试在图2右边空白处画出面积为 的长方形的示意图（标注好a、b），由图形可知，多项式  可分解因式为：                          ．

在上方空白处画出②中的示意图

③ 若将代数式 展开后合并同类项，得到多项式N，则多项式N的项数一共有                          项.

（1） 当a＝3，b＝2时，分别求代数式（a＋b）²和a²＋2ab＋b²的值，并观察这两个代数式的值有什么关系？
（2）再多找几组你喜欢的数试一试，从中你发现了什么规律？
（3）利用你所发现的规律计算a＝1. 625，b＝0. 375时，a²＋2ab＋b²的值？

（x-2）（x-3）=x²-5x+6；

（x+5）（x-2）=x²+3x-10；

（x+3）（x+6）=x²+9x+18；

（x+9）（x-10）=x²-x-90；

……