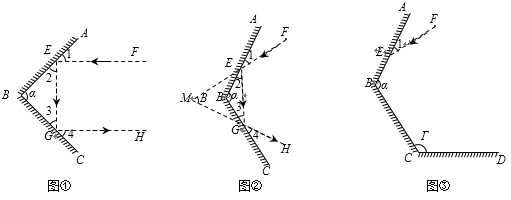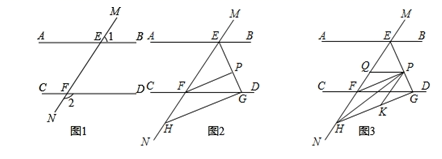
①求 的度数范围;
② 与
度数的和是否变化?若不变,请求出
与
的度数和;若变化,请说明理由.



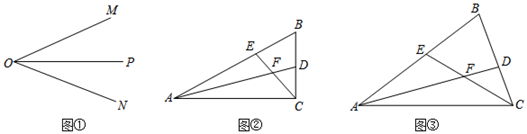
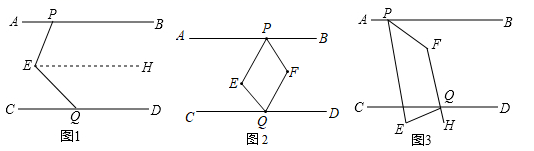
已知直线AB//CD,点E在AB,CD之间,点P,Q分别在直线AB,CD上,连接PE,EQ.
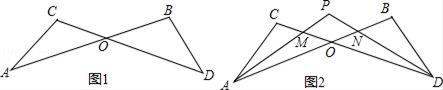
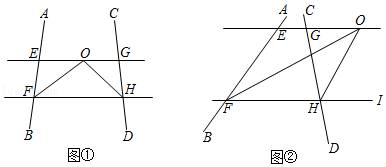
①以线段AC为边的“8字型”有_▲_个,以点O为交点的“8字型”有_▲_个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAP= ∠CAB,∠CDP=
∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
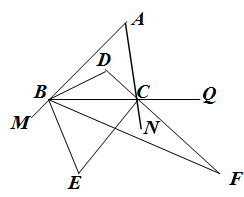
①∠BDC的度数为 .
②求∠BEC的度数.
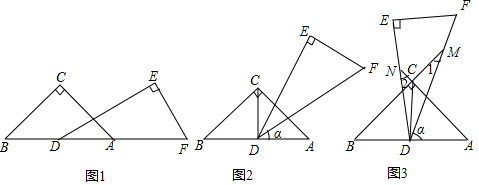
①此时∠α的度数范围是 ▲ ;
②∠1与∠2度数的和是否变化?若不变求出∠1与∠2度数和;若变化,请说明理由;
③若使得∠2≥2∠1,求∠α的度数范围.

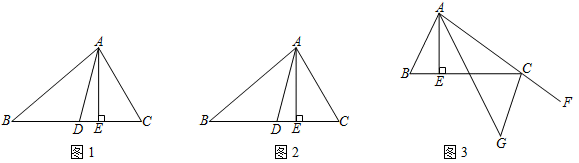
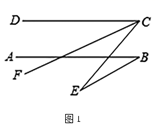
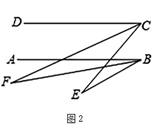
①若 y=70,s=10,t=20,则 x=;
②探究 s、t、x、y 之间的数量关系,并证明你得到的结论.
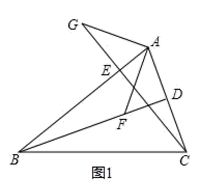
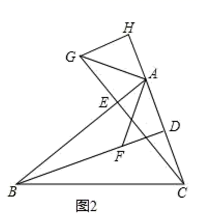
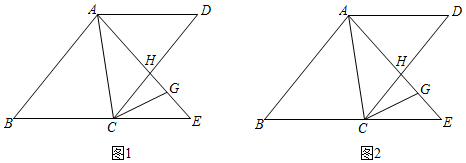
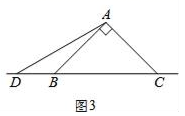
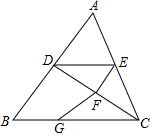
如图,在 中,
分别是
边上的高,在
上截取
延长
至点
使
,连接
.