北京市海淀区2020-2021学年八年级下学期期末数学试题

更新时间：2024-07-13 浏览次数：153 类型：期末考试

一、单选题

1. (2024八下·海珠期中) 计算 $\text{[math]}$ 的结果为（）

A . 3 B . $\text{[math]}$ C . 6 D . 9

答案解析收藏纠错 + 选题
2. (2024九上·丰台开学考) 以下列长度的三条线段为边，能组成直角三角形的是（）

A . 1；1；1 B . 2；3；4 C . 1； $\text{[math]}$ ；2 D . $\text{[math]}$ ；3；5

答案解析收藏纠错 + 选题
3. (2022八下·台江期末) 把直线y＝3x向下平移2个单位，得到的直线是（）

A . y＝3x﹣2 B . y＝3（x﹣2） C . y＝3x+2 D . y＝3（x+2）

答案解析收藏纠错 + 选题
4. (2023八下·通州期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . 40° B . 50° C . 60° D . 70°

答案解析收藏纠错 + 选题
5. (2021八下·海淀期末) 一家鞋店在一段时间内销售了某种女鞋40双，各种尺码的鞋的销售量如表所示：
尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量/双
1
2
5
7
14
8
3
店主再进一批女鞋时，打算多进尺码为24 cm的鞋，你认为他做这个决定是重点关注了下列统计量中的（）

A . 平均数 B . 中位数 C . 众数 D . 方差

答案解析收藏纠错 + 选题
6. (2021八下·海淀期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 边上的高 $\text{[math]}$ 的长为（）

A . 4 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021八下·海淀期末) 如图，一次函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象交于点P，则关于x，y的方程组 $\text{[math]}$ 的解是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021八下·海淀期末) 如图，在平面直角坐标系 $\text{[math]}$ 中，矩形 $\text{[math]}$ 的顶点A，C的坐标分别是 $\text{[math]}$ ， $\text{[math]}$ ，点B在x轴上，则点B的横坐标是（）

A . 4 B . $\text{[math]}$ C . 5 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023八下·北京市期中) 如图，在实践活动课上，小华打算测量学校旗杆的高度，她发现旗杆顶端的绳子垂到地面后还多出1m，当她把绳子斜拉直，且使绳子的底端刚好接触地面时，测得绳子底端距离旗杆底部5m，由此可计算出学校旗杆的高度是（）

A . 8m B . 10m C . 12m D . 15m

答案解析收藏纠错 + 选题
10. 如图，有一个球形容器，小海在往容器里注水的过程中发现，水面的高度h、水面的面积S及注水量V是三个变量．下列有四种说法：①S是V的函数；②V是S的函数；③h是S的函数；④S是h的函数．其中所有正确结论的序号是（）

A . ①③ B . ①④ C . ②③ D . ②④

答案解析收藏纠错 + 选题

二、填空题

11. (2024九上·北京市开学考) 若二次根式 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是．

答案解析收藏纠错 + 选题
12. (2022八下·台江期末) 函数 $\text{[math]}$ （k是常数， $\text{[math]}$ ）的图象上有两个点 $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ ，写出一个满足条件的函数解析式：．

答案解析收藏纠错 + 选题
13. (2023九上·东莞开学考) 如图， $\text{[math]}$ ， $\text{[math]}$ 两点被池塘隔开，在 $\text{[math]}$ 外选一点 $\text{[math]}$ ，连接 $\text{[math]}$ 和 $\text{[math]}$ ．分别取 $\text{[math]}$ ， $\text{[math]}$ 的中点 $\text{[math]}$ ， $\text{[math]}$ ，测得 $\text{[math]}$ ， $\text{[math]}$ 两点间的距离为 $\text{[math]}$ ，则 $\text{[math]}$ 、 $\text{[math]}$ 两点间的距离为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024九下·银川模拟) 一个水库的水位在最近5h内持续上涨，下表记录了这5h内6个时间点的水位高度，其中t表示时间，y表示水位高度．
t/h
0
1
2
3
4
5
y/m
3
3.3
3.6
3.9
4.2
4.5
据估计这种上涨规律还会持续2h，预测再过2h水位高度将为m．

答案解析收藏纠错 + 选题
15. (2024九上·丰台开学考) 在平面直角坐标系xOy中，直线 $\text{[math]}$ （ $\text{[math]}$ ）与直线 $\text{[math]}$ ，直线 $\text{[math]}$ 分别交于A，B两点．若点A，B的纵坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
16. (2021八下·海淀期末) 某校八年级有600名学生，为了解他们对安全与环保知识的认识程度，随机抽取了30名学生参加安全与环保知识问答活动．此活动分为安全知识和环保知识两个部分．这30名学生的安全知识成绩和环保知识成绩如图所示．根据下图，判断安全知识成绩的方差 $\text{[math]}$ 和环保知识成绩的方差 $\text{[math]}$ 的大小： $\text{[math]}$ $\text{[math]}$ （填“＞”，“＝”或“＜”）．

答案解析收藏纠错 + 选题

三、解答题

17. (2022八下·台江期末) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2024八下·惠州期末) 如图，在 $\text{[math]}$ 中，点E，F分别在BC，AD上，且 $\text{[math]}$ ，连接AE，CF．求证：AE//CF．

答案解析收藏纠错 + 选题
19. (2021八下·海淀期末) 下面是小明设计的“过直线外一点作已知直线的平行线”的尺规作图过程．
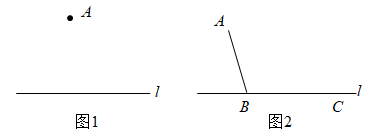
已知：如图1，直线l 及直线l 外一点A．
求作：直线AD，使得AD// l．
作法：如图2，
①在直线l 上任取两点B，C，连接AB；
②分别以点A，C 为圆心，线段BC，AB 长为半径画弧，两弧在直线l 上方相交于点D；
③作直线AD．
直线AD 就是所求作的直线．
根据小明设计的尺规作图过程，
1. （1）使用直尺和圆规，补全图形（保留作图痕迹）；
2. （2）完成下面的证明．
  证明：连接CD．
  ∵ AB ＝▲ ， BC ＝▲ ，
  ∴ 四边形ABCD 为平行四边形（）（填推理的依据）．
  ∴ AD// l．
答案解析收藏纠错 + 选题
20. (2021八下·海淀期末) 在平面直角坐标系 $\text{[math]}$ 中，一次函数的图象经过点 $\text{[math]}$ 与 $\text{[math]}$ ．
1. （1）求这个一次函数的解析式；
2. （2）若点C是x轴上一点，且 $\text{[math]}$ 的面积是5，求点C的坐标．
答案解析收藏纠错 + 选题
21. (2021八下·海淀期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为边 $\text{[math]}$ 上的中线，点E与点D关于直线 $\text{[math]}$ 对称，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是菱形；
2. （2）连接BE，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
22. (2021八下·海淀期末) 第24届冬季奥林匹克运动会将于2022年2月4日至2月20日在中国北京和张家口市联合举行．为了解学生对冬奥会冰雪项目的认识程度，某校体育组老师从该校八年级学生中随机抽取了20名学生进行冰上项目和雪上项目的知识测试，获得了他们的测试成绩（百分制），并对数据（测试成绩）进行整理、描述和分析．下面给出了部分信息．
a．测试成绩的频数分布表如下：
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
冰上项目
0
0
12
6
2
雪上项目
1
4
7
3
5
b．雪上项目测试成绩在 $\text{[math]}$ 这一组的是：
70，70，70，71，71，73，75
c．冰上项目和雪上项目测试成绩的平均数、中位数、众数如下：
项目
平均数
中位数
众数
冰上项目
77.95
76
75
雪上项目
76.85
m
70
根据以上信息，回答下列问题：
1. （1）表中m的值为；
2. （2）在此次测试中，某学生的冰上项目测试成绩为75分，雪上项目测试成绩为73分，这名学生测试成绩排名更靠前的是（填“冰上”或“雪上”）项目，并说明理由；
3. （3）已知该校八年级共有200名学生，假设该年级学生都参加此次测试，估计冰上项目测试成绩不低于80分的人数．
答案解析收藏纠错 + 选题
23. (2021八下·海淀期末) 在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于点A．
1. （1）求点A的坐标；
2. （2）当 $\text{[math]}$ 时，直接写出x的取值范围；
3. （3）已知直线 $\text{[math]}$ ，当 $\text{[math]}$ 时，对于x的每一个值，都有 $\text{[math]}$ ，直接写出k的取值范围．
答案解析收藏纠错 + 选题
24. (2021八下·海淀期末) 在正方形 $\text{[math]}$ 中，F是线段 $\text{[math]}$ 上一动点（不与点B，C重合），连接 $\text{[math]}$ ， $\text{[math]}$ ，分别过点F，C作 $\text{[math]}$ ， $\text{[math]}$ 的垂线交于点Q．
1. （1）依题意补全图形，并证明 $\text{[math]}$ ；
2. （2）过点Q作 $\text{[math]}$ ∥ $\text{[math]}$ ，交 $\text{[math]}$ 于点N，连接 $\text{[math]}$ ．若正方形 $\text{[math]}$ 的边长为1，写出一个 $\text{[math]}$ 的值，使四边形 $\text{[math]}$ 为平行四边形，并证明．
答案解析收藏纠错 + 选题
25. (2021八下·海淀期末) 在平面直角坐标系 $\text{[math]}$ 中，对于点 $\text{[math]}$ 与 $\text{[math]}$ ，给出如下的定义：
将过点 $\text{[math]}$ 的直线记为 $\text{[math]}$ ，若直线 $\text{[math]}$ 与 $\text{[math]}$ 有且只有两个公共点，则称这两个公共点之间的距离为直线 $\text{[math]}$ 与 $\text{[math]}$ 的“穿越距离”，记作 $\text{[math]}$ ．

例如，已知过点 $\text{[math]}$ 的直线 $\text{[math]}$ 与 $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，如图所示，则 $\text{[math]}$ ．

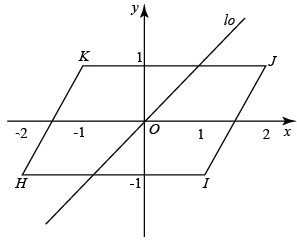
请解决下面的问题：

已知 $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 时，已知 $\text{[math]}$ ， $\text{[math]}$ 为过点 $\text{[math]}$ 的直线 $\text{[math]}$ ．
  ①当 $\text{[math]}$ 时， $\text{[math]}$ _ ▲ ；当 $\text{[math]}$ 时， $\text{[math]}$ ▲ ；
  
  ②若 $\text{[math]}$ ，结合图象，求 $\text{[math]}$ 的值；
2. （2）已知 $\text{[math]}$ ， $\text{[math]}$ 为过点 $\text{[math]}$ 的直线，若 $\text{[math]}$ 有最大值，且最大值为 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题