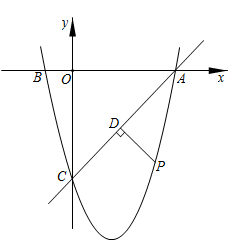
B .
B .  C .
C .  D .
D . 
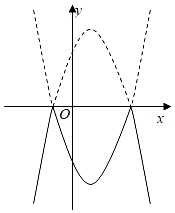


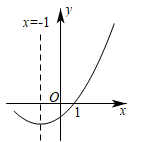
① ;
② ;
③关于x的一元二次方程 的两根分别为-3和1;
④若点 ,
,
均在二次函数图象上,则
;
⑤ (m为任意实数).
其中正确的结论有( )

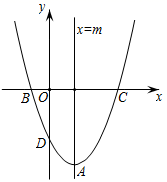
① ;②若
,则
;③对于任意
,始终有
;④若B的坐标为
,则C的坐标为
.
速度v(千米/小时) | … | 5 | 10 | 20 | 32 | 40 | 48 | … |
流量q(辆/小时) | … | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | … |
①市交通运行监控平台显示,当 时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值