
 B .
B .  C .
C .  D .
D . 





⑴画出△ABC关于原点O成中心对称的图形;
⑵P(a,b)是△ABC的AC边上一点,将△ABC平移后点P的对称点 , 请画出平移后的
;⑶若
和
关于某一点成中心对称,则对称中心的坐标为 ▲ .

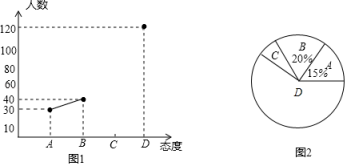
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.63 | 0.62 | 0.593 | a | 0.601 | 0.599 | b |
|
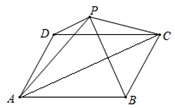
平行四边形的性质定理3:行四边形的对角线互相平分。 我们可以用演绎推理证明这个结论。 已知:如图, 求证:OA=OC,OB=OD。
|
证明:

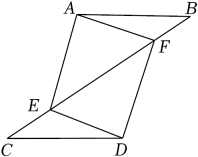
【性质应用】
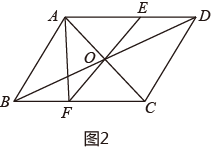
如图2,的对角线
相交于点
,
过点
且与
分别相交于点
,

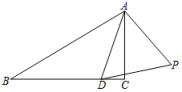
如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE.则:
①∠AEB的度数为°;
②线段AD、BE之间的数量关系是.
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点 A、D、E在同一直线上,若AD=a,AE=b,AB=c,求a、b、c之间的数量关系.
图1中的△ACB和△DCE,在△DCE旋转过程中,当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索∠AOE的度数,直接写出结果,不必说明理由.
