江西省赣州市瑞金市2022年九年级下学期中考模拟数学试题

更新时间：2022-04-27 浏览次数：85 类型：中考模拟

一、单选题

1. (2018·福田模拟) -3的相反数是（）

A . -3 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 下列计算或运算中，正确的是（）

A . a⁶÷a²＝a³ B . (－2a²)³＝－8a⁸ C . (a－3)(3＋a)＝a²－9 D . (a－b)²＝a²－b²

答案解析收藏纠错 + 选题
3. (2020九上·息县期末) 下列图形中，既是中心对称图形又是轴对称图形的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
4. 如图，直线a∥b，c、d是截线且交于点A，若∠1 ＝ 55°，∠2 ＝ 100 °，则∠A＝（）

A . 40° B . 45° C . 55° D . 65°

答案解析收藏纠错 + 选题
5. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，弦 $\text{[math]}$ ，垂足为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. 如图，将边长为 $\text{[math]}$ 的正方形绕点B逆时针旋转30°，那么图中阴影部分的面积为（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

7. 使式子 $\text{[math]}$ 有意义的x的取值范围是．

答案解析收藏纠错 + 选题
8. 因式分解： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
9. (2020七上·前郭期末) 随着“一带一路”建设的不断发展，我国已与多个国家建立了经贸合作关系．去年中哈铁路（中国至哈萨克斯坦）运输量达8200000吨，将8200000用科学记数法表示为．

答案解析收藏纠错 + 选题
10. (2019九上·宁都期中) 等腰三角形三边长分别为 $\text{[math]}$ ，且 $\text{[math]}$ 是关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的两根，则 $\text{[math]}$ 的值为

答案解析收藏纠错 + 选题
11. 如图，直线AB，AD与⊙O分别相切于点B、D两点，C为⊙O上一点，且∠BCD＝140°，则∠A的度数是

答案解析收藏纠错 + 选题
12. 已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，给下以下结论：①2a﹣b=0； ②abc＞0 ③4ac﹣b²＜0； ④9a+3b+c＜0； ⑤8a+c＜0．其中正确的结论有

答案解析收藏纠错 + 选题

三、解答题

13.
1. （1）计算： $\text{[math]}$
2. （2）化简： $\text{[math]}$
答案解析收藏纠错 + 选题
14. 如图点E，F分别是矩形ABCD的边AD，AB上一点，若AE=DC=2ED，且EF⊥EC
1. （1）求证：点F为AB的中点．
2. （2）延长EF与CB的延长线相交于点H，连接AH，已知ED=2，求AH的值．
答案解析收藏纠错 + 选题
15. 先化简： $\text{[math]}$ ，然后，m在1，2，3中选择一个合适的数代入求值．

答案解析收藏纠错 + 选题
16. 按要求作图，不要求写作法，但要保留作图痕迹
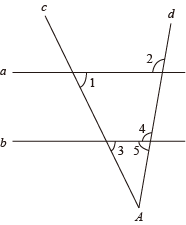
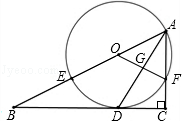
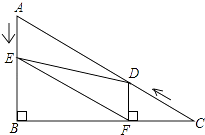
我们知道，三角形具有性质，三边的垂直平分线相交于同一点，三条角平分线相交于一点，三条中线相交于一点，事实上，三角形还具有性质：三条高交于同一点，请运用上述性质，只用直尺（不带刻度）作图：
1. （1）如图2，在▱ABCD中，E为CD的中点，作BC的中点F；
2. （2）图3，在由小正方形组成的网格中，△ABC的顶点都在小正方形的顶点上，作△ABC的高AH
答案解析收藏纠错 + 选题
17. (2021九上·九江期末) 某校准备从八年级1班、2班的团员中选取两名同学作为运动会的志愿者，已知1班有4名团员（其中男生2人，女生2人）.2班有3名团员（其中男生1人，女生2人）．
1. （1）如果从这两个班的全体团员中随机选取一名同学作为志愿者的组长，则这名同学是男生的概率为；
2. （2）如果分别从1班、2班的团员中随机各选取一人，请用画树状图或列表的方法求这两名同学恰好是一名男生、一名女生的概率．
答案解析收藏纠错 + 选题
18. 家庭过期药品属于“国家危险废物”，处理不当将污染环境，危害健康．某校学生杨杨和舟舟为了解市民家庭处理过期药品的方式，决定对全市家庭作一次简单随机抽样调查．
1. （1）下列选取样本的方法最合理的一种是．（只需填上符合题意答案的序号）
  ①在市中心某个居民区以家庭为单位随机抽取；
  ②在全市医务工作者中以家庭为单位随机抽取；
  ③在全市常住人口中以家庭为单位随机抽取．
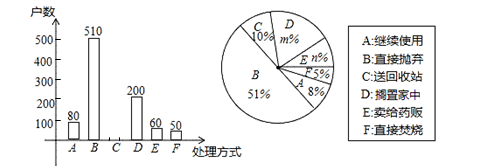
2. （2）本次抽样调查发现，接受调查的家庭都有过期药品，现将有关数据呈现如图：
  ①m= ▲ ；n= ▲ ；
  ②补全条形统计图；
  ③根据调查数据，你认为该市市民家庭处理过期药品最常见的方式是 ▲ ；
  ④家庭过期药品的正确处理方式是送回收站点，若该市有180万户家庭，请估计大约有多少户家庭处理过期药品的方式是送回收站点．
答案解析收藏纠错 + 选题
19. 如图，在平面直角坐标系中，直线 $\text{[math]}$ （ $\text{[math]}$ ）与双曲线 $\text{[math]}$ （ $\text{[math]}$ ）交于A、B两点，已知点A(m，2)，点B(－1，－4)．
1. （1）求直线和双曲线的解析式；
2. （2）把直线y₁沿x轴负方向平移2个单位后得到直线 y₃ ，直线y₃与双曲线y₂交于D、E两点，当y₂＞y₃时，求x 的取值范围．
答案解析收藏纠错 + 选题
20. 如图所示的是一款机械手臂，由上臂、中臂和底座三部分组成，其中上臂和中臂可自由转动，底座与水平地面垂直．在实际运用中要求三部分始终处于同一平面内，其示意图如图1所示，经测量，上臂 $\text{[math]}$ ，中臂 $\text{[math]}$ ，底座 $\text{[math]}$
1. （1）若上臂 $\text{[math]}$ 与水平面平行， $\text{[math]}$ ．计算点 $\text{[math]}$ 到地面的距离．
2. （2）在一次操作中，中臂与底座成 $\text{[math]}$ 夹角，上臂与中臂夹角为 $\text{[math]}$ ，如图2，计算这时点 $\text{[math]}$ 到地面的距离．与图1状态相比，这时点A向前伸长了多少?
答案解析收藏纠错 + 选题
21. 如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，O为AB上一点，经过点A，D的⊙O分别交AB，AC于点E，F，连接OF交AD于点G．
1. （1）求证：BC是⊙O的切线；
2. （2）设AB＝x，AF＝y，试用含x，y的代数式表示线段AD的长；
3. （3）若BE＝8，sinB＝ $\text{[math]}$ ，求DG的长，
答案解析收藏纠错 + 选题
22. 如图，在等腰三角形ABC中，∠BAC＝90°，点A在x轴上，点B在y轴上，点C(3，1)，二次函数y＝ $\text{[math]}$ x²＋bx－ $\text{[math]}$ 的图象经过点C．
1. （1）求二次函数的解析式，并把解析式化成y＝a(x－h)²＋k的形式；
2. （2）把△ABC沿x轴正方向平移，当点B落在抛物线上时，求△ABC扫过区域的面积；
3. （3）在抛物线上是否存在异于点C的点P，使△ABP是以AB为直角边的等腰直角三角形？如果存在，请求出所有符合条件的点P的坐标；如果不存在，请说明理由．
答案解析收藏纠错 + 选题
23. (2011·河南) 如图，在Rt△ABC中，∠B=90°，BC=5 $\text{[math]}$ ，∠C=30°．点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连接DE、EF．
1. （1）求证：AE=DF；
2. （2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．
3. （3）当t为何值时，△DEF为直角三角形？请说明理由．
答案解析收藏纠错 + 选题