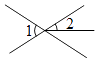重庆市江津区12校联盟学校2021-2022学年七年级下学期...

更新时间：2022-04-30 浏览次数：109 类型：期中考试

一、选择题（每小题4分，共48分）

1. (2023七下·徐闻期中) 下面四个图形中，∠1 与∠2是对顶角的图形是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2022七下·江津期中) 点A（3，-5）在（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. (2022七下·江津期中) 通过平移，可将图中的福娃“欢欢”移动到图（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022七下·江津期中) 在实数 $\text{[math]}$ ，0， $\text{[math]}$ ，-3.14， $\text{[math]}$ 中，无理数有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
5. (2022七下·江津期中) 如图，直线l₁与l₂相交于点O，OM⊥l₁ ，若β=44°，则a为（）

A . 44° B . 45° C . 46° D . 56°

答案解析收藏纠错 + 选题
6. (2024七下·南昌期中)
如图所示，点E在AC的延长线上，下列条件中能判断AB∥CD（　　）

A . ∠1=∠2 B . ∠3=∠4 C . ∠D=∠DCE D . ∠D+∠ACD=180°

答案解析收藏纠错 + 选题
7. (2022七下·江津期中) 一个自然数的算术平方根是x，则下一个自然数的算术平方根是（）

A . $\text{[math]}$ +1 B . $\text{[math]}$ C . $\text{[math]}$ D . x+1

答案解析收藏纠错 + 选题
8. (2022七下·江津期中) 如图a∥b，∠1与∠2互余，∠3=115°，则∠4等于（）

A . 115° B . 155° C . 135° D . 125°

答案解析收藏纠错 + 选题
9. (2022七下·江津期中) 如图，数轴上A，B两点所对应的实数分别是-1、 $\text{[math]}$ ，若线段AB= BC，则点C所表示的实数是（）

A . 1+ $\text{[math]}$ B . 2+ $\text{[math]}$ C . 2 $\text{[math]}$ +1 D . 2 $\text{[math]}$ -1

答案解析收藏纠错 + 选题
10. (2024七下·海安月考) 已知点P在第二象限，且到x轴的距离是2，到y轴的距离是3，则点P的坐标为（）

A . （2，3） B . （-2，3） C . （-3，2） D . （3，-2）

答案解析收藏纠错 + 选题
11. (2024七下·恩施期中) 如图，把一张长方形纸条ABCD沿EF折叠，若∠1=56°，则∠EGF应为（）

A . 68° B . 34° C . 56° D . 不能确定

答案解析收藏纠错 + 选题
12. (2022七下·江津期中) 如图，△ABC中，AH⊥BC，BF平分∠ABC，BE L BF，EF∥BC，以下四个结论①AH⊥EF，②∠ABF=∠EFB，③AC∥BE，④∠E=∠ABE．正确的是（）

A . ①②③④ B . ①② C . ①③④ D . ①②④

答案解析收藏纠错 + 选题

二、填空题（每小题4分，共16分）

13. (2022七下·十堰期中) $\text{[math]}$ 的平方根是， $\text{[math]}$ 的算术平方根是

答案解析收藏纠错 + 选题
14. (2022七下·江津期中) 把命题“平行于同一条直线的两条直线互相平行”改写成“如果……，那么……”形为

答案解析收藏纠错 + 选题
15. (2024七下·江油期中) 如图，计划把河水引到水池A中，先引AB⊥CD，垂足为B，然后沿AB开渠，能使所开的渠道最短，这样设计的依据是

答案解析收藏纠错 + 选题
16. (2022七下·江津期中) 在平面直角坐标系中，点A₁（1，0），A₂（2，3），A₃（3，8），A₄（4，15），……，用你发现的规律确定点A_n的坐标为

答案解析收藏纠错 + 选题

三、解答题（共16分）

17. (2022七下·江津期中) 计算
1. （1） $\text{[math]}$
2. （2） x²-81=0
答案解析收藏纠错 + 选题
18. (2022七下·江津期中) 已知，如图，∠1=∠2，∠3=∠4，试说明EG∥FH的道理，以下是说明道理的过程，请将其填写完整，并在括号内填出所得结论的理由。

解：∵∠1=∠2（已知）
∠AEF=∠1（                  ）

∴∠AEF=∠2（                 ）

∴AB∥CD（                 ）

∴∠BEF=∠CFE （                 ）

∵∠3=∠4（                 ）

∴∠BEF-∠4=∠CFE-∠3（                 ）

即∠GEF=∠（                 ）

∴EG∥FH（                 ）

答案解析收藏纠错 + 选题

四、解答题（共40分）

19. (2022七下·江津期中) 化简求值：
2x²y-[3xy²-3（ $\text{[math]}$ x²y+xy）]+4xy²的值，且x，y满足（x- $\text{[math]}$ ）+|y+1|=0．

答案解析收藏纠错 + 选题
20. (2022七下·江津期中) 如图，OA⊥OB，∠BOC=50°，且∠AOD：∠COD=4：7，OE为∠BOC的平分线，求出∠DOE的度数．

答案解析收藏纠错 + 选题
21. (2022七下·江津期中) 如图所示，已知AB∥DC，AE平分∠BAD，CD与AE相交于点F，∠CFE=∠E，试说明AD∥BC．

答案解析收藏纠错 + 选题
22. (2022七下·江津期中) 如图，DE⊥AC于点E，BF⊥AC于点F，∠1+∠2=180°，试判断∠AGF与∠ABC的大小关系，并说明理由。

答案解析收藏纠错 + 选题

五、解答题（共30分）

23. (2022七下·江津期中) 若实数a，b，c在数轴．上所对应点分别为A，B，C，a为2的算术平方根，b=3，C点与A点在B点的两侧，并且点A与点C到B点的距离相等.
1. （1）求数轴上AB两点之间的距离；
2. （2）求c点对应的数；
3. （3） a的整数部分为x，c的小数部分为y，求2x³+2y的值（结果保留带根号的形式）；
答案解析收藏纠错 + 选题
24. (2022七下·江津期中) 阅读下列解题过程：
$\text{[math]}$

$\text{[math]}$

请回答下列问题：
1. （1）观察上面的解答过程，请写出 $\text{[math]}$
2. （2）利用上面的解法，请化简：
  $\text{[math]}$
3. （3）比较大小： $\text{[math]}$ 和 $\text{[math]}$ 。
答案解析收藏纠错 + 选题
25. (2022七下·江津期中) 如图1，E是直线AB、CD内部一点，AB∥CD，连接EA，ED．
1. （1）探究猜想：
  ①若∠A=20°，∠D=50°，则∠AED= ▲ 度；
  
  ②若∠A=35°，∠D=45°，则∠AED= ▲ 度；
  
  ③猜想图1中∠AED、∠EAB、∠EDC的数量关系并证明你的结论．
2. （2）拓展应用：
  如图2，射线FE与长方形ABCD的边AB交于点E，与边CD交于点F，①②③④分别是被射线FE隔开的4个区域（不含边界，其中区域③、④位于直线AB上方），P是位于以上四个区域上的点，猜想：∠PEB，∠PFC，∠EPF的关系（直接写出结论，不要求证明）
答案解析收藏纠错 + 选题