11.
(2022·普陀模拟)
2021年5月7日,《科学》杂志发布了我国成功研制出可编程超导量子计算机“祖冲之”号的相关研究成果.祖冲之是我国南北朝时期杰出的数学家,他是第一个将圆周率

精确到小数点后第七位的人,他给出

的两个分数形式:

(约率)和

(密率).同时期数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数

的不足近似值和过剩近似值分别为

和

(即有

,其中

,

,

,

为正整数),则

是

的更为精确的近似值.例如:已知

,则利用一次“调日法”后可得到

的一个更为精确的近似分数为:

;由于

,再由

,可以再次使用“调日法”得到

的更为精确的近似分数……现已知

,则使用两次“调日法”可得到

的近似分数为
.
 B .
B .  C .
C .  D .
D . 
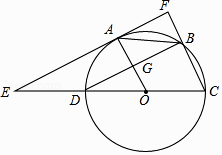
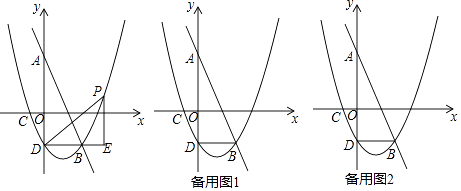
的数量关系是,
的大小为;
绕点A顺时针方向旋转到如图2所示的位置,连接
判断
的形状,并说明理由;
绕点A在平面内自由旋转,若
,请求出
面积的最大值.